
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства функции распределения
|
|
|
|
1). Значения функции распределения принадлежат отрезку 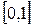 :
:

Это свойство вытекает из определения функции распределения как вероятности: вероятность всегда есть число неотрицательное, не превышающее единицы.
2). 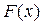 - функция неубывающая, т.е.
- функция неубывающая, т.е.  если
если 
Доказательство. Пусть  Событие, состоящее в том, что
Событие, состоящее в том, что  , можно представить в виде двух событий: 1)
, можно представить в виде двух событий: 1) 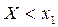 с вероятностью
с вероятностью  2)
2) 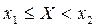 , с вероятностью
, с вероятностью  . По теореме сложения вероятностей имеем
. По теореме сложения вероятностей имеем
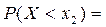
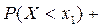
 .
.
Отсюда 


Или 
 . (*)
. (*)
Так как любая вероятность есть число неотрицательное, то 
или  что и требовалось доказать.
что и требовалось доказать.
Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале 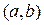 , равна приращению функции распределения на этом интервале:
, равна приращению функции распределения на этом интервале: 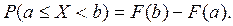 (**)
(**)
Это важное следствие вытекает из формулы (*) при 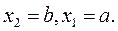
Следствие 2. Вероятность того, что непрерывная случайная величина  примет одно определенное значение, равна нулю.
примет одно определенное значение, равна нулю.
Положив в формуле (**) 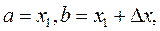 имеем
имеем
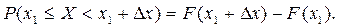
Разность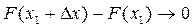 при
при 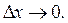
3) Если возможные значения случайной величины принадлежат интервалу 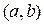 , то: 1)
, то: 1)  при
при 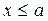 ; 2)
; 2) 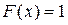 при
при 
Доказательство. 1) Пусть 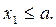 Тогда событие
Тогда событие  невозможно, т.к. значений, меньших
невозможно, т.к. значений, меньших  , величина
, величина  по условию не принимает, и, следовательно вероятность его равна нулю.
по условию не принимает, и, следовательно вероятность его равна нулю.
2) Пусть  Тогда событие
Тогда событие  достоверно, т.к. все возможные значения
достоверно, т.к. все возможные значения  меньше
меньше  , и, следовательно, вероятность его равно единице (входят в интервал
, и, следовательно, вероятность его равно единице (входят в интервал 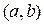 ).
).
Следствие. Если возможные значения непрерывной случайной величины расположены на оси  , то справедливы следующие предельные соотношения:
, то справедливы следующие предельные соотношения:

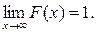
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 324; Нарушение авторских прав?; Мы поможем в написании вашей работы!