Плотность совместного распределения вероятностей непрерывной двумерной случайной величины (двумерная плотность вероятности)

Кроме функции распределения, непрерывную двумерную величину

можно также задать, пользуясь плотностью распределения. Будем предполагать, что функция распределения 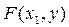всюду непрерывна и имеет (за исключением, быть может, конечного числа точек) непрерывную частную производную второго порядка.

Плотностью совместного распределения вероятностей

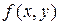двумерной непрерывной случайной величины 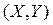называют

вторую смешанную частную производную от функции распределения:

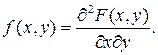
Геометрически эту функцию можно истолковать как поверхность, которую

называют поверхностью распределения.

Пример. Найти плотность совместного распределения 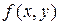системы

случайных величин 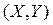по известной функции распределения

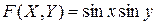
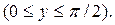
Найдем частную производную по 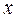от функции распределения:

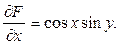
От полученного результата найдем производную по и найдем искомую

плотность совместного распределения:

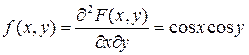
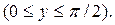
Дата добавления: 2014-01-06