Линейная регрессия. Прямые линии среднеквадратической регрессии

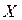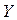Пусть двумерная случайная величина, где и зависимые случайные величины с точностью функции , т.е. . Предположим, что зависимость между величинами линейная с точностью до неизвестных параметров и :

.

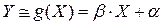Параметры и могут быть определены различными способами: наиболее распространенный из них – это метод наименьших квадратов.

Функцию называют “наилучшим” приближением 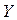в смысле метода наименьших квадратов, если математическое ожидание 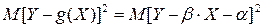принимает наименьшее возможное значение. При этом функцию 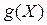называют среднеквадратической регрессией 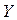на .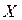

Теорема. Линейная средняя квадратическая регрессия 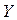на 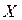имеет вид

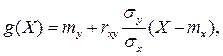
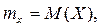
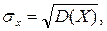
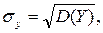
где -коэффициент корреляции величин 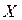и .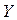

Доказательство. Введем в рассмотрение функцию двух независимых параметров и :

.

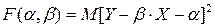Учитывая, что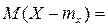

и выполнив выкладки, получим

(*)

Исследуем функцию на экстремум, для чего приравниваем нулю частные производные:

Отсюда (**)

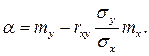Подставив (**) в (*) можно убедиться, что функция 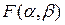принимает наименьшее значение.

Итак, линейная средняя квадратическая регрессия 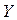на 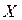имеет вид

Коэффициент 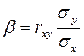называют коэффициентом регрессии 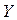на 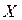, а прямую

(**)

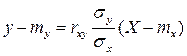называют прямой среднеквадратической регрессии 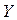на .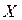

Подставив найденные значения и в соотношение (*), получим минимальное значение 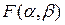=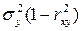. Величину 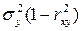называют остаточной дисперсией случайной величины 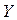относительно случайной величины 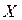. Остаточная дисперсия характеризует величину ошибки, которую допускают при замене 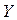линейной функцией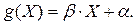

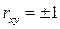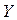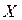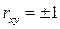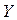При остаточная дисперсия равна нулю; при этих крайних значениях коэффициента корреляции не возникает ошибки при представлении в виде линейной функции от . То есть, если коэффициент корреляции , то и 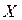связаны линейной функциональной зависимостью.

Аналогично можно получить прямую среднеквадратической регрессии 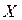на :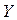

, (***)

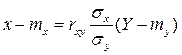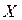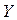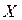где - коэффициент регрессии на ; остаточную дисперсию величины относительно .

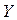Если 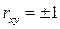, то обе прямые регрессии (**) и (***) совпадают.

Обе прямые регрессии проходят через точку , которую называют центром совместного распределения величин 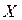на .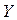

Дата добавления: 2014-01-06