Импульс системы частиц

По определению, импульс частицы (другое название этой величины — количество движения) .

Уравнение (1.3.7) позволяет найти приращение импульса час­тицы за любой промежуток времени, если известна зависи­мость силы от времени. Действительно, из (1.3.7) следует, что элементарное приращение импульса частицы за промежуток времени dt есть d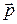= 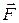dt. Проинтегрировав это выражение по времени, найдем приращение импульса частицы за конечный промежуток времени t:

(1.4.1)

Величину, стоящую в правой части этого уравнения, назы­вают импульсом силы. Таким образом, приращение импульса частицы за любой промежуток времени зависит не только от значения силы, но и от продолжительности ее действия, или, другими словами, равно импульсу силы за это время.

Теперь рассмотрим произвольную систему частиц. В общем случае частицы этой системы могут взаимодействовать как между со­бой, так и с телами, не входящими в данную систему. В соот­ветствии с этим силы взаимодействия между частицами систе­мы называют внутренними, а силы, обусловленные действием других тел, не входящих в данную систему, — внешними. Такое разделение сил на внутренние и внешние условно — оно целиком зависит от выбора интересующей нас системы частиц.

Импульс системы это векторная сумма импульсов ее отдельных частиц:

(1.4.2)

где 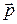_i — импульс i-ой частицы. Заметим, что импульс систе­мы — величина аддитивная, т. е. импульс системы равен сумме импульсов ее отдельных частей независимо от того, взаимодей­ствуют они между собой или нет.

Найдем физическую величину, которая определяет измене­ние импульса системы. Для этого продифференцируем (1.4.2) по времени: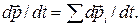

Согласно (1.3.7),

где 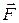_ik — силы, действующие на i-ую частицу со стороны других частиц системы (внутренние силы); 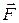_i — сила, действующая на эту же частицу со стороны других тел, не входящих в рассмат­риваемую систему (внешние силы). Подставив последнее выра­жение в предыдущее, получим

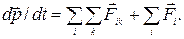
Двойная сумма справа — это сумма всех внутренних сил. В соответствии с третьим законом Ньютона силы взаимодействия между частицами системы попарно одинаковы по модулю и противоположны по направлению. Поэтому результирующая сила в каждой паре взаимодействия равна нулю, а значит, рав­на нулю и векторная сумма всех внутренних сил. В результате последнее уравнение принимает следующий вид:

(1.4.3)

где 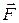_внеш — результирующая всех внешних сил.

Дата добавления: 2014-01-06