Преобразование скоростей

Пусть в K-системе в плоскости X, Y движется частица со скоростью v, проекции которой u_x и u_y. С помощью преобразований Лоренца находятся проекции скорости этой частицы 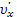и 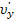в K’‑системе, движущейся со скоростью V.

(1.10.7)

где b = V/c. Отсюда скорость частицы в K’-системе

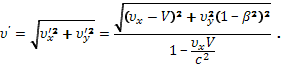
Эти формулы выражают релятивистский закон преобразования скорости. При малых скоростях (V «c и u «c) они переходят, как нетрудно убедиться, в формулы преобразования скорости ньютоновской механики:

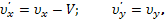
Релятивистский импульс.

Напомним сначала два основных положения ньютоновской механики об импульсе:

1) импульс частицы определяется как , где масса m частицы считается не зависящей от ее скорости;

2) импульс замкнутой системы частиц сохраняется во времени в любой инерциальной системе отсчета.

Теперь обратимся к релятивистской динамике. Оказывается для замкнутой системы из релятивистских частиц закон сохранения ньютоновского импульса не выполняется. Возникает альтернатива: отказаться или от ньютоновского определения импульса, или от закона сохранения этой величины.

Учитывая громадную роль, которую играют законы сохранения, в теории относительности за фундаментальный принимают именно закон сохранения импульса и уже отсюда находят выражение для самого импульса.

При этом оказывается, что требование, чтобы закон сохранения импульса выполнялся в любой инерциальной системе отсчета, и учет релятивистского преобразования скоростей при переходе от одной инерциальной системы отсчета к другой приводят к выводу, что масса частицы должна зависеть от ее скорости (в отличие от ньютоновской механики):

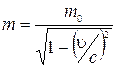. (1.10.8)

Здесь m — «масса» движущейся частицы, 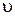- ее скорость, 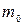- масса неподвижной частицы, которую называют массой покоя. Величину т называют релятивистской массой. Она, как видно из формулы (1.10.8), больше массы покоя и зависит от скорости частицы. Другими словами, релятивистская масса одной и той же частицы различна в разных инерциальных системах отсчета.

В отличие от релятивистской массы масса покоя m₀ частицы — величина инвариантная, т. е. одинаковая во всех системах отсчета. По этой причине именно масса покоя является характеристикой частицы. В дальнейшем, однако, мы будем использовать и релятивистскую массу m, имея в виду при этом, что m представляет собой просто сокращенное обозначение отношения 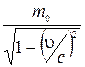, и не более. Использование релятивистской массы продиктовано только стремлением упростить ряд выводов, рассуждений и расчетов.

Массу покоя m₀ будем называть в дальнейшем просто массой.

Теперь сделаем последний шаг — напишем выражение для импульса релятивистской частицы. С учетом (1.10.8) этот импульс записывают в виде

(1.10.9)

Это и есть релятивистский импульс частицы. Опыт подтверждает, что так определенный импульс действительно подчиняется закону сохранения независимо от выбора инерциальной системы отсчета.

Отметим, что при u «c из (1.10.9) следует ньютоновское определение импульса: 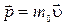, где m₀ не зависит от скорости u.

Чтобы удовлетворить требованиям принципа относительности, основное уравнение динамики должно иметь другой вид и лишь при u «c переходить в ньютоновское уравнение. Этим требованиям, как доказывается в теории относительности, удовлетворяет уравнение

(1.10.10)

где 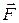— сила, действующая на частицу. Данное уравнение по виду полностью совпадает с основным уравнением ньютоновской динамики. Однако физический смысл здесь уже другой: слева стоит производная по времени от релятивистского импульса, определяемого формулой (1.10.9). Подставив (1.10.9) в (1.10.10), получим

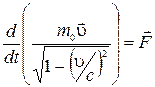(1.10.11)

Это и есть основное уравнение релятивистской динамики.

В таком виде уравнение динамики приводит к сохранению импульса для свободной частицы и при малых скоростях (u «c) принимает форму основного уравнения ньютоновской динамики (m).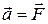

Кроме того, именно в таком виде основное уравнение динамики оказывается инвариантным по отношению к преобразованиям Лоренца и, следовательно, удовлетворяет принципу относительности Эйнштейна. Не останавливаясь на способе доказательства этого, отметим только, что при переходе от одной инерциальной системы отсчета к другой необходимо принять, что сила 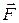преобразуется по определенным законам. Другими словами, сила 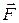в теории относительности — величина неинвариантная, в разных системах отсчета ее числовое значение и направление будут различны.

Из основного уравнения релятивистской динамики следует неожиданный вывод: вектор ускорения частицы в общем случае не совпадает по направлению с вектором силы 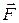. Чтобы это показать, запишем (1.10.10) в такой форме:

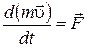
где m — релятивистская масса частицы. Выполнив дифференцирование по времени, получим

. (1.10.12)

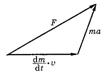Это выражение графически представлено на рис.1.10.2. Таким образом, действительно, вектор ускорения в общем случае не колинеарен вектору силы.

Рис.1.10.2.

Кинетическая энергия релятивистской частицы.

Запишем приращение кинетической энергии dK частицы под действием силы 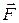на элементарном пути d= 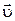dt:

.

Если использовать соотношения (1.10.10) и (1.10.8), можно получить

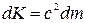. (1.10.13)

Таким образом, приращение кинетической энергии частицы пропорционально приращению ее релятивистской массы. Кинетическая энергия покоящейся частицы равна нулю, а ее релятивистская масса m = m₀. Поэтому, проинтегрировав (1.10.13), получим

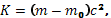(1.10.14)

или

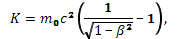(1.10.15)

где b = u/c. Это и есть выражение для релятивистской кинетической энергии частицы. Оно сильно отличается от ньютоновского m₀u²/2. При малых скоростях (b «1) выражение (1.10.15) переходит в ньютоновское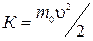

Таким образом, при больших скоростях кинетическая энергия частицы определяется релятивистской формулой (1.10.15), отличной от m₀u²/2. Заметим, что (1.10.15) нельзя представить и в виде mu²/2, где m — релятивистская масса.

Дата добавления: 2014-01-06