Идеальный и реальный газ

Лекция 1.15

Уравнение состояния идеального газа.

Идеальным называется газ, взаимодействие между молекулами которого пренебрежимо мало. Реальный газ при достаточном разрежении близок по своим свойствам к идеальному. Идеальный газ одно из двух идеальных систем,

для которых можно строго вывести уравнение состояния. Для всех других систем уравнения состояния получают эмпирически.

Рассмотрим идеальный газ, заключенный в сосуде. Молекулы газа непрерывно соударяются с его стенками, в результате чего оказывают давление на них. Рассмотрим взаимодействие молекул с одной стенкой (рис.1.15.1).

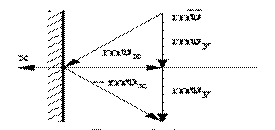
Рис.1.15.1.

Вследствие хаотичности движения молекул давление газа на различные участки стенок сосуда одинаково. Давление газа на стенки определяется

р=(суммарная сила взаимодействия молекул со стенкой) / (площадь стенки)

Молекулы соударяются со стенкой упруго, т.е. отскакивают от стенки зеркально (углы падения и отражения равно). В результате взаимодействия с одной молекулой, массы т, движущейся со скоростью 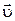, стенка, расположенная перпендикулярно оси х, получает импульс 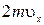. Поскольку все направления движения равновероятны, за время dt со стенкой площадью столкнется dN молекул, имеющих составляющую скорости 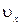, dN = 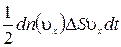, где - число молекул в единице объема, имеющих скорости в интервале 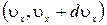. Величина 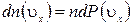, п – концентрация молекул, 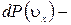вероятность молекулам иметь скорость в указанном интервале. Тогда сила соударения молекул, имеющих скорость в указанном интервале, с единичной площадкой стенки = 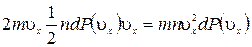и полное давление всех молекул, соударяющихся с этой стенкой

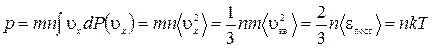. (1.15.1)

Выражение получено с учетом (1.14.11).

Это и есть уравнение состояния идеального газа:

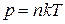. (1.15.2)

Это уравнение можно записать иначе, если учесть , , 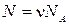(N - полное число молекул, 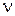- число молей газа, 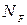- число Авогадро, R - универсальная газовая постоянная)

. (1.15.3)

Внутренняя энергия идеального газа.

Поскольку в идеальном газе отсутствуют силы взаимодействия между молекулами, то внутренняя энергия идеального газа представляет собой только кинетическую энергию молекул

, (1.15.4)

где i - число степеней свободы молекулы, которое равно 3 для одноатомной молекулы, 5 – для двухатомной, 6 – для многоатомной.

Теплоемкости и уравнение политропы идеального газа.

Из соотношений (1.13.5), (1.13.6), и (1.15.4) получим выражения для молярной теплоемкости при постоянном объеме и постоянном давлении идеального газа: 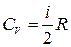, . (1.15.5)

Для получения уравнения политропы воспользуемся формулой (1.13.8). Из уравнения состояния (1.15.3) получим и . Подставив эти значения в (1.13.8), получим . Проинтегрировав это равенство, будем иметь . (1.15.6)

В частности, уравнение адиабатного процесса

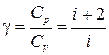(1.15.7)

Энтропия идеального газа.

Из соотношений (1.14.4), (1.12.7), (1.13.5) и (1.12.4) следует

.

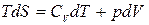Для идеального газа 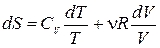. После интегрирования получим

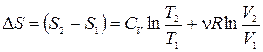. (1.15.8)

Реальный газ. Уравнение Ван – дер – Вальса.

В реальных газах между молекулами существуют как силы притяжения, которые преобладают на далеких расстояниях, так и силы отталкивания, которые преобладают при сближении молекул. Действие сил отталкивания сводится к тому, что молекула не допускает проникновения в некоторый объем других молекул. Следовательно, силы отталкивания характеризуются эффективным объемом молекулы. Наличие сил притяжения приводит к появлению дополнительного внутреннего давления.

Как уже говорилось, уравнение состояния реального газа нельзя получить аналитически. Существует несколько различных уравнений, описывающих состояние реального газа. Все они получены эмпирически. Чаще всего состояние реального газа описывают уравнением Ван – дер – Вальса, которое в достаточно широком диапазоне изменения параметров дает удовлетворительное согласие с экспериментом. Для моля реального газа оно имеет вид:

. (1.15.9)

Параметры а и b называются постоянными Ван – дер – Вальса. Они зависят от рода газа.

Изотермы Ван-дер-Ваальса

Достоинство уравнения Ван – дер - Ваальса состоит не только в том, что оно описывает газовую фазу вещества в более широкой области температур и давления, но и в том, что оно описывает картину превращения газа в жидкость. Для объяснения этого факта рассмотрим зависимости давления от объема при постоянной температуре (изотермы).

Преобразуем уравнение Ван – дер - Ваальса для одного моля и запишем его по степеням объема

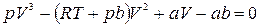. (1.15.10)

Уравнение состояния стало кубическим относительно объёма, а число постоянных, являющихся его параметрами, стало равным трем. Как известно, кубическое уравнение имеет три корня. Для уравнения Ван-дер-Ваальса имеют место три следующих случая: а) корни действительны; б) два корня мнимые и один корень действительный, в) три действительных корня тождественны.

На рис.1.15.2 схематически изображены изотермы газа Ван-дер-Ваальса для различных температур.

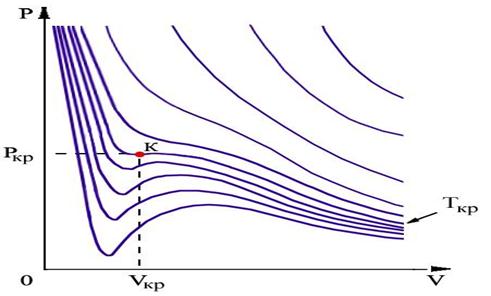
Рис.1.15.2.    

На части этих изотерм хорошо просматривается участок, где давление растёт с ростом объёма. Этот участок не имеет физического смысла. В области, где изотерма делает зигзагообразный изгиб, изобара пересекает её три раза, то есть, имеется три значения объёма 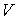при одинаковых значениях параметров p и . Это соответствует существованию трёх действительных корней уравнения (1.15.10). При повышении температуры волнообразный участок уменьшается и превращается в точку (точка К на рис.1.15.10). Эта точка называется критической, а значения 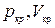и в этой точке называются критическими параметрами. Критической точке соответствуют три совпадающих корня уравнения (1.15.10). При температурах, превышающих критическую, изотермы Ван-дер-Ваальса становятся монотонно убывающими функциями р(V).

Критические параметры , и 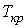можно найти из условия, что в критической точке изотерма Ван-дер-Ваальса имеет точку перегиба. Из этого условия можно получить

.

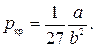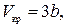Таким образом, из уравнения состояния газа Ван-дер-Ваальса следует существование у реальных газов критической точки с параметрами , и 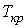, величина которых зависит от свойств газа.

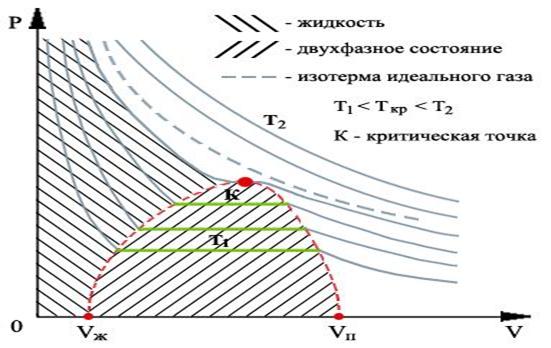
Обратимся теперь к экспериментальным кривым изотерм Ван-дер-Ваальса. На рис.1.15.3 показан вид экспериментально полученных изотерм, характерный для многих веществ.

Рис.1.15.3.

На этих кривых виден горизонтальный участок, который заменяет немонотонный участок на теоретических изотермах газа Ван-дер-Ваальса (рис.1.15.2). Справа от горизонтального участка давление на экспериментальной изотерме монотонно растет с уменьшением объема, что соответствует сжатию реального газа при постоянной температуре. Горизонтальный участок соответствует сжижению газа, которое при заданной температуре происходит при постоянном давлении. При этом существует двухфазная система жидкость-газ. Наконец, слева от горизонтального участка, где изотерма вновь становится монотонно убывающей функцией , весь газ превращается в жидкость. При этом давление очень резко растет с уменьшением объема. Это связано с тем, что межмолекулярные расстояния становятся сравнимы с размерами молекул, что приводит к малой сжимаемости жидкостей.

Совокупность участков изотерм реального газа, соответствующих двухфазным системам жидкость-газ, образуют колоколообразную фигуру (см. рис.1.15.3), вершиной которой является критическая точка. выше критической вещество может существовать только в газообразном состоянии. При температуре ниже критической, вещество может быть сжижено. Таким образом, на диаграмме можно указать три области значений параметров, при которых вещество может существовать только в газообразном, только в жидком состояниях и область, где жидкость и газ находятся в равновесии.

Например, критическая температура для гелия очень низкая - 5,2 К. Поэтому его сжижение связано с большими трудностями. В отличие от гелия, водорода, кислорода и азота, чьи критические температуры достаточно низкие (поэтому в основном они существуют в газообразном состоянии), такие вещества как вода и ртуть (критические температуры 647 К и 1820 К соответственно) существуют как в жидком, так и в газообразном состояниях при комнатных температурах. Поэтому исчезает различие понятий "газ" и "пар".При температурах

Внутренняя энергия реального газа.

Для нахождения внутренней энергии газа Ван-дер-Ваальса, воспользуемся следующим приемом. Пусть над газом Ван-дер-Ваальса осуществляется процесс без теплообмена с окружающей средой. Тогда изменение его внутренней энергии можно записать в виде

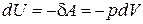. (1.15.11)

При тех же условиях изменение внутренней энергии идеального газа можно было бы рассчитать по формуле

. (1.15.12)

Сравнивая уравнения состояния моля идеального (1.15.3) и реального (1.15.9) газов, можем видеть и 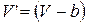, что после подстановки в (1.15.12) дает

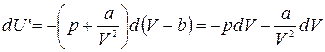
Первое слагаемое в правой части этого выражения согласно формуле (1.15.11) представляет собой изменение внутренней энергии газа Ван-дер-Ваальса. Отсюда следует:

.

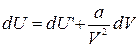Интегрирование этого выражения дает

.

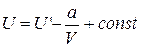Здесь произвольную константу интегрирования необходимо положить равной нулю, так как при выражения для внутренних энергий газа Ван-дер-Ваальса и идеального газа должна совпадать: .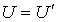

Использование выражения (1.15.4) для внутренней энергии идеального газа позволяет записать формулу, для расчета внутренней энергии одного моля газа Ван- дер – Вальса

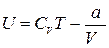. (1.15.13)

Как следует из этого выражения, внутренняя энергия газа Ван-дер-Ваальса зависит не только от его температуры, как в случае с идеальным газом, но и от объема, занимаемого им. По этой причине, при осуществлении изотермических процессов в газе Ван-дер-Ваальса, будет изменяться его внутренняя энергия, а, следовательно, при таких процессах подведенная к газу теплота не будет равна совершенной им работе.

Если внутренняя энергия идеального газа определяется кинетической энергией его молекул, то для газа Ван-дер-Ваальса существенное значение имеет потенциальная энергия, обусловленная силами притяжения и отталкивания.

Дата добавления: 2014-01-06