Связь полюсов и нулей

Полюсы

Пусть не существует конечного предела . Если = , то особая точка называется полюсом функции .

Точка называется нулем функции , если .

Теорема. Для того чтобы точка была полюсом функции , необходимо и достаточно, чтобы она была нулем функции .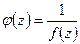

Доказательство. Необходимость. Пусть - полюс функции , тогда аналитическая в , а = , то есть

Тогда функция аналитическая в и ограничена в окрестности точки . Поэтому точка - правильная точка функции и существует конечный . В силу произвольности 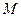=0. - нуль функции .

Достаточность. Пусть - нуль функции (- правильная точка функции ) и аналитическая в .

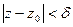Тогда 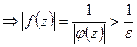. Следовательно, =и - полюс функции .

Примеры.

1. 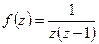. Так как точки 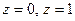- нули функции , то точки 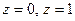полюсы функции .

2. . Так как , то 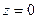- полюс функции .

Будем считать аналитической в

Точка называется полюсом n–го порядка функции , если .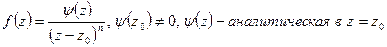

Точка называется нулем n–го порядка функции , если ,

.

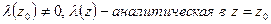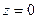Пример. . Точка - полюс пятого порядка, 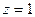- полюс третьего порядка, - полюс второго порядка..

Теорема. Для того чтобы точка была полюсом функции n-го порядка, необходимо и достаточно, чтобы она была нулем n-го порядка функции .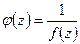

Доказательство. Необходимость. Пусть точка полюс функции n-го порядка, тогда , =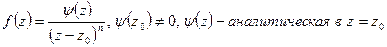

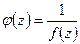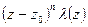, где 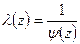. Так как - аналитическая в и , то - аналитическая в и , поэтому точка - нуль n-го порядка функции .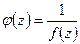

Достаточность доказать самостоятельно (доказательство аналогично).

Теорема. Для того чтобы точка 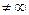была полюсом n-го порядка функции , необходимо и достаточно, чтобы ее разложение в ряд Лорана по степеням 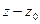не содержало степеней ниже (-n) и содержало слагаемое .

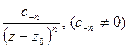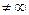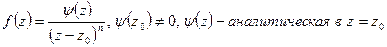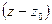Доказательство. Необходимость. Если точка - полюс n-го порядка функции , то . Разложим аналитическую функцию в ряд Тейлора по степеням и подставим разложение. . .

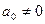Достаточность. Пусть . Тогда

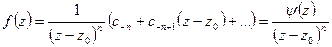, где 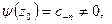- аналитическая в точке функция (как сумма степенного ряда). Поэтому - полюс n-го порядка функции .

Существенно особая точка.

Если вообще не существует , ни конечного, ни бесконечного, то особая точка называется существенно особой точкой функции .

Теорема. Разложение функции в ряд Лорана в окрестности существенно особой точки конечной плоскости содержит бесконечное количество отрицательных степеней .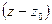

Доказательство. Если разложение в ряд Лорана в окрестности особой точки конечной плоскости не содержит отрицательных степеней, то точка - правильная (доказанная выше теорема) - противоречие. Если разложение в ряд Лорана содержит конечное число отрицательных степеней, то точка - полюс (.доказанная выше теорема) - противоречие. Остается только вариант наличия в разложении бесконечного числа слагаемых с отрицательными степенями.

Теорема Сохоцкого. Каково бы ни было число А, конечное или бесконечное, существует такая последовательность 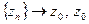- существенно особая точка функции , что .

Доказательство. 1) Пусть A – конечное число. Предположим, что не существует последовательности, о которой идет речь в теореме. Тогда значения функции отделены от A, т.е. . Рассмотрим функцию .

Из предыдущей оценки следует, что в 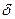- окрестности точки , т.е. ограничена, следовательно, - правильная точка функции . Поэтому существует конечный предел .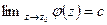

a) Пусть 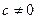. Выразим через . . Тогда = 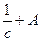- конечное число. Следовательно, - правильная точка функции - противоречие.

b) Пусть . .

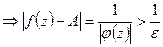Тогда 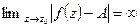, т.е. - полюс . Противоречие.

2) Пусть . Надо доказать, что при . Пусть для любой последовательности 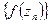не стремится к бесконечно удаленной точке. Тогда для любой последовательности 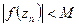, следовательно, функция ограничена в окрестности , тогда - правильная точка - противоречие.

Классификация особой точки (конечной плоскости) функции по ее разложению в ряд Лорана в окрестности этой точки.

Если разложение функции в ряд Лорана в окрестности (по степеням ):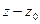

1. Не содержит отрицательных степеней, то - правильная точка .

2. Содержит конечное число отрицательных степеней, то - полюс , причем наинизшая отрицательная степень определяет порядок полюса.

3. Содержит бесконечное количество членов с отрицательными степенями, то - существенно особая точка .

Это следует из доказанных выше теорем.

Классификация бесконечно удаленной особой точки 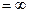функции по ее разложению в ряд Лорана в окрестности этой точки.

Разложение в ряд Лорана в окрестности точки 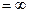, т.е. в области представляет собой ряд Лорана по степеням z: , в котором главная часть, определяющая особенности функции, содержит положительные степени, а правильная часть – отрицательные степени.

Если разложение в ряд Лорана в окрестности точки 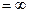, т.е. в области :

1 Не содержит положительных степеней, то 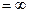- правильная точка .

2 Содержит конечное число положительных степеней, то 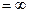- полюс , причем наивысшая положительная степень определяет порядок полюса.

3 Содержит бесконечное количество членов с положительными степенями, то 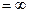- существенно особая точка .

Примеры.

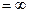1 . Это и есть разложение в ряд Лорана в окрестности точки , т.е. в области , поэтому 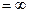- полюс второго порядка.

2 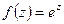. Разложение по степеням : 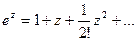справедливо в области , т.е. в окрестности точки 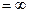. Оно содержит бесконечное количество членов с положительными степенями, поэтому 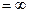- существенно особая точка .

3 . Запишем разложение в окрестности точки 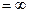, т.е. в области .

. Разложение не содержит положительных степеней , поэтому точка 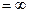- правильная, точнее, нуль первого порядка.

4. 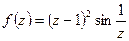. Запишем разложение по степеням в окрестности точки .

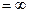В разложении старшая положительная степень – первая, поэтому 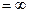- полюс первого порядка. Это же разложение справедливо в области 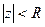, поэтому оно является разложением в окрестности точки 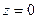. В нем бесконечное количество отрицательных степеней, поэтому точка 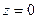- существенно особая.

Дата добавления: 2014-01-06