Общая (третья) теорема разложения

Пусть 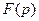- аналитическая за исключением конечного числа особых точек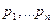 . Пусть 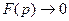при 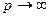, равномерно по аргументу . Тогда .

Доказательство. Пусть в область, ограниченную 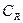и отрезком, соединяющим точки 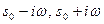, попало m из n особых точек. По общей теореме о вычетах

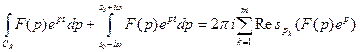. Устремим 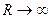. Внутрь рассматриваемой области войдут тогда все n особых точек. К первому слагаемому может быть применена лемма Жордана, его предел при 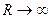.будет равен нулю. Ко второму слагаемому может быть применена теорема обращения. Его предел при 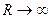.будет равен . Следовательно, в результате предельного перехода получим, сокращая обе части на , .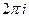

Дата добавления: 2014-01-06