Методом операционного исчисления

Решение дифференциальных уравнений и систем

Лекция 4.

Следствие. Вторая теорема разложения.

Пусть имеет в качестве особых точек только полюсы 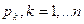кратности . Тогда

Доказательство теоремы сводится к применению общей теоремы разложения и формулы вычисления вычета в полюсе порядка.

При решении дифференциальных уравнений и систем используется теорема о дифференцировании оригинала и ее следствие – теорема об изображении n-ой производной.

Метод решения основан на том, что преобразование Лапласа сводит дифференцирование в пространстве оригиналов к умножению на p в пространстве изображений. Поэтому дифференциальное уравнение с постоянными коэффициентами с пространстве оригиналов переходит в алгебраическое уравнение в пространстве изображений. При этом учитываются и начальные условия, что удобно при решении задачи Коши.

Получив решение алгебраического уравнения в пространстве изображений, мы получаем решение в виде некоторого изображения – функции от p. Остается найти соответствующий ему оригинал по свойствам преобразования Лапласа (теоремам подобия, смещения, запаздывания, дифференцирования и интегрирования) или теоремам разложения.

Пусть задано дифференциальное уравнение с постоянными коэффициентами 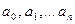относительно неизвестной функции и ее производных с правой частью – функцией , являющейся оригиналом

.

Требуется решить задачу Коши для этого уравнения при начальных условиях .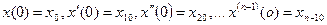

Применим преобразование Лапласа к обеим частям равенства.

.

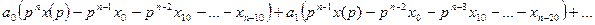
Приведем коэффициенты при 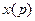в левой части и перенесем члены, зависящие от начальных условий, в правую часть.

,

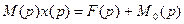где 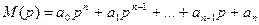- характеристический многочлен,

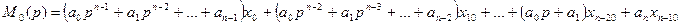Найдем изображение решения

.

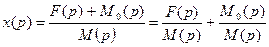Здесь первое слагаемое дает вклад правой части в решение, второе слагаемое – вклад начальных условий. Если начальные условия нулевые, то и второе слагаемое пропадает.

Примеры.

1.

,

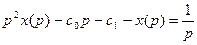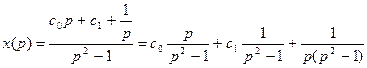
Первые два слагаемых соответствуют , оригинал для третьего слагаемого находим по теореме об интегрировании оригинала: .

.

2.

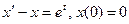
по теореме о дифференцировании изображения.

3.

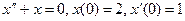
4.

.

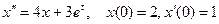
Если свертку вычислить трудно, то можно найти оригинал для последнего слагаемого по теореме разложения.

=.

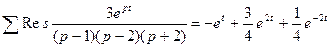Дата добавления: 2014-01-06