Сводка теории. Элементарной конъюнкцией называется конъюнкция переменных или их отрицаний, в которой каждая переменная или ее отрицание встречаются не более одного раза

Элементарной конъюнкцией называется конъюнкция переменных или их отрицаний, в которой каждая переменная или ее отрицание встречаются не более одного раза.

Всякая дизъюнкция элементарных конъюнкций называется дизъюнктивной нормальной формой (ДНФ).

Следует отметить, что ДНФ функции (или формулы) может быть не единственной.

Алгоритм приведения к ДНФ может быть описан с привлечением приведенных ранее равносильностей или основных логических законов (см. разд. 1.2). Сначала с помощью закона (II.1) и законов де Моргана (II.2), (II.3) все отрицания «спускаются» до переменных. Затем раскрываются скобки, с помощью логических законов (I.7), (I.8), (IV.7) и (IV.8) удаляются лишние конъюнкции и повторения переменных в конъюнкциях, а с помощью логических законов (IV.1.) – (IV.6) удаляются константы.

Элементарная конъюнкция называется правильной, если в нее каждая переменная входит не более одного раза (включая ее вхождения под знаком отрицания).

Правильная элементарная конъюнкция называется полной относительно переменных 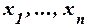, если каждая из этих переменных входит в нее один и только один раз (может быть, под знаком отрицания).

Совершенной дизъюнктивной нормальной формой (СДНФ) относительно переменных 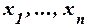называется ДНФ, в которой нет одинаковых элементарных конъюнкций и все элементарные конъюнкции правильны и полны относительно переменных .

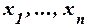Поскольку из вида СДНФ бывают ясны ее переменные, будем говорить просто СДНФ, опуская слова: «относительно переменных ».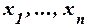

Всякую ДНФ можно привести к СДНФ расщеплением конъюнкций, которые содержат не все переменные, например:

.

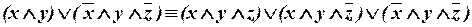Если из формулы F с помощью некоторых равносильностей можно получить формулу Ф, то F можно получить из Ф, используя те же равносильности. Это соображение позволяет доказать следующую теорему.

Теорема 1.1

Для любых двух равносильных формул F и Ф существует тождественное преобразование F в Ф с помощью соотношений (I.1.) – (IV.8).

Замечание

Важность этой теоремы в том, что соотношений (I.1.) – (IV.8) оказывается достаточно для любого тождественного преобразования в булевой алгебре.

Аналогично ДНФ определяется конъюнктивная нормальная форма (КНФ) как конъюнкция элементарных дизъюнкций.

Переход от ДНФ к КНФ можно осуществить следующим образом. Пусть ДНФ F имеет вид: 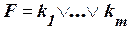, где 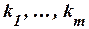– элементарные конъюнкции. Формула 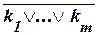приводится к ДНФ .

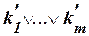Тогда 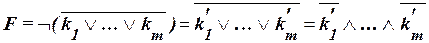. По законам Де Моргана отрицания элементарных конъюнкций преобразуются в элементарные дизъюнкции, что и даст КНФ.

Аналогом СДНФ является совершенная конъюнктивная нормальная форма (СКНФ), каждая элементарная дизъюнкция которой содержит все переменные. Построение СКНФ из КНФ проводится аналогично тому, как из ДНФ получается СДНФ.

Таким образом, любая формула алгебры логики высказываний может быть записана в СДНФ (кроме тождественно-ложной) или в СКНФ (кроме тождественно-истинной).

Дата добавления: 2014-01-06