Замечания

Определение

Формула называется тождественно-истинной (тождественно-ложной), если при любом замещении входящих в нее предикатных символов конкретными предикатами она переходит в тождественно-истинный (тождественно-ложный) предикат (если она не замкнута) или в истинное (ложное) высказывание (если она замкнута).

1) Тождественно-истинная формула и тождественно-истинный предикат – не одно и то же. Тождественная истинность конкретного предиката относится только к его области определения, в то время как тождественная истинность формулы – это «абсолютная истинность», истинность для любых предметных областей. Аналогично – для тождественной ложности.

2) Из определения непосредственно следует, что формула 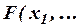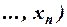со свободными переменными 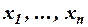тождественно-истинна тогда и только тогда, когда тождественно-истинна формула .

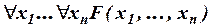3) Отрицание тождественно-истинной формулы есть, очевидно, формула тождественно-ложная, а отрицание тождественно-ложной – тождественно-истинная.

Для расширения возможностей тождественных преобразований формул логики предикатов используются основные свойства кванторов.

I) Перестановка одноименных кванторов:

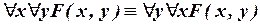; (I.1)

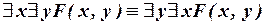. (I.2)

2) Связь между разноименными кванторами:

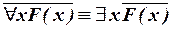; (II.1)

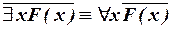. (II.2)

3) Вынесение кванторов за скобки:

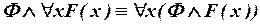;	(где Ф не содержит свободной переменной x)	(III.1)
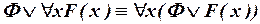;	(III.2)
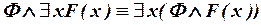;	(III.3)
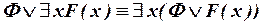.	(III.4)

Замечание

Условие, чтобы формула Ф не содержала свободной переменной x, в соотношениях (III.1 – III.4) является существенным: если оно не выполнено, то соотношения могут нарушаться (после вынесения квантора переменная x в формуле Ф из свободной может превратиться в связанную).

4) Переименование связанных переменных:

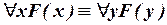;	(вместо x и y можно брать любые другие переменные)	(IV.1)
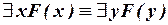.	(IV.2)

Замечание

Все введенные равносильности останутся справедливыми, если заменить в них F(x) (соответственно F(x, y)) любой формулой G, содержащей свободную переменную x (соответственно x и y) и, возможно, также и другие свободные переменные.

Отметим в общем виде самый простой из частных случаев, когда для доказательства равносильности формул логики предикатов удается воспользоваться средствами логики высказываний.

Утверждение 2.1

Если в равносильных формулах логики высказываний заменить элементарные высказывания произвольными предикатными символами так, чтобы одно и то же элементарное высказывание заменялось в обеих формулах одним и тем же символом, то возникающие при этом формулы логики предикатов будут также равносильны.

Утверждение 2.2

Если в тождественно-истинной формуле логики высказываний заменить элементарные высказывания произвольными предикатными символами, то возникающая при этом формула логики предикатов также тождественно-истинна (то же справедливо для тождественно-ложных формул).

С помощью свойств кванторов можно производить над формулами логики предикатов тождественные преобразования, причем ввиду утверждения 2.1 в этих преобразованиях можно использовать также любые равносильности логики высказываний. Производя тождественные преобразования в определенном порядке, можно для каждой формулы получить ей равносильную, имеющую особенно простое строение.

Дата добавления: 2014-01-06