Основы специальной теории относительности

Вынужденные колебания

Вынужденными колебаниями называются колебания, происходящие под действием внешней переменной (периодической) силы, работа которой компенсирует потери энергии на преодоление трения (в механических колебательных системах) и на преодоление электрического сопротивления (в электрических колебательных системах).

Раздел 3. Основы специальной теории относительности /1а, 1б, 3б/

(2 часа)

Лекция 10.

Основы специальной теории относительности.

Постулаты Специальной Теории Относительности Эйнштейна

• Принцип относительности: ВСЕ ЗАКОНЫ ПРИРОДЫ ОДИНАКОВЫ ВО ВСЕХ ИНЕРЦИАЛЬНЫХ СИСТЕМАХ ОТСЧЕТА

• Принцип постоянства скорости света: СКОРОСТЬ СВЕТА В ВАКУУМЕ ОДИНАКОВА ВО ВСЕХ ИНЕРЦИАЛЬНЫХ СИСТЕМАХ ОТСЧЕТА И НЕ ЗАВИСИТ ОТ ДВИЖЕНИЯ ИСТОЧНИКОВ И ПРИЕМНИКОВ СВЕТА

c = 2,9979246·10⁸ м/с ≈ 3·10⁸ м/с

Преобразования координат и времени

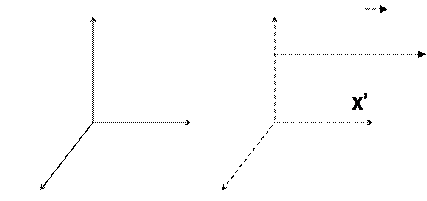(1) При t = t’ = 0 начала координат обеих систем совпадают: x₀ = x’₀’ = x₀’ = x’₀ = 0

(2) x_0’ = v₀·t (2’) x’₀ = – v₀·t’

Чтобы выполнялись (1) и (2), для любой точки должно быть:

(3) x = γ·(x’ + v₀·t’) (3’) x’ = γ·(x – v₀·t)

Пусть при t = t’ = 0 в начале координат произойдет вспышка света.

После этого будет двигаться «фронт световой волны» - граница светлой и темной зон пространства

Поскольку системы координат равноправны, а скорость света одинакова в обеих системах координат, то координата «фронта»:

(4) x = c·t; (4’) x’ = c·t’

(3) x = γ·(x’ + v₀·t’) (3’) x’ = γ·(x – v₀·t)

(4) x = c·t; (4’) x’ = c·t’

(5) c·t = γ·(c·t’ + v₀·t’) (5’) c·t’ = γ·(c·t – v₀·t)

Вынесем за скобки время и перемножим (5) и (5’)

c² = γ²·(c² – v₀²)

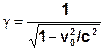
Дата добавления: 2014-01-06