Представление числовой информации с помощью систем счисления

Хранение информации.

Носители информации:

· ОЗУ компьютера (оперативная память).

· Гибкие диски 3,5”

· Оптические диски CD, DVD и др.

· Жёсткие диски.

· Переносные запоминающие устройства – flash и др.

Передача информации: источник, приёмник, канал.

Обработка информации: компьютер и др.

ТЕМА 2 ”Представление информации в компьютерах”

Простейшие способы представления данных:

1. Последовательность символов (текст);

2. Вещественные и целые числа (числовые данные);

3. Изображения (графика, фотографии, рисунки, схемы);

4. Звук (речь, музыка);

5. Видео (фильм, анимация).

Существует множество систем представления данных. Наиболее распространенная из них основана на использовании двух цифр – 0 и 1. С помощью этих цифр можно выразить два понятия – да или нет, истина или ложь, наличие электрического импульса или отсутствие и т.п.

Информация, представленная в виде последовательности нулей и единиц, называется машинным кодом, а такой способ представления информации – кодированием двоичным ( бинарным ) кодом. Широкое применение двоичного кода в вычислительной технике обусловлено его простотой и надежностью.

Компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:

· для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;

· представление информации посредством только двух состояний надежно и помехоустойчиво;

· возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;

· двоичная арифметика намного проще десятичной.

Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел.

Для записи информации о количестве объектов использу­ются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисле­ния. Алфавит систем счисления состоит из символов, кото­рые называются цифрами. Например, в десятичной системе счисления числа записываются с помощью десяти всем хо­рошо известных цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Система счисления — это знаковая система, в ко­торой числа записываются по определенным пра­вилам с помощью символов некоторого алфавита, называемых цифрами.

Все системы счисления делятся на две большие группы: позиционные и непозиционные системы счисления. В пози­ционных системах счисления значение цифры зависит от ее положения в числе, а в непозиционных — не зависит.

Римская непозиционная система счисления. Самой рас­пространенной из непозиционных систем счисления являет­ся римская. В качестве цифр в ней используются: I (1), V (5), X (10), L (50), С (100), D (500), М (1000).

Значение цифры не зависит от ее положения в числе. На­пример, в числе XXX (30) цифра Х встречается трижды и в каждом случае обозначает одну и ту же величину - число 10, три числа по 10 в сумме дают 30.

Величина числа в римской системе счисления определя­ется как сумма или разность цифр в числе. Если меньшая цифра стоит слева от большей, то она вычитается, если справа - прибавляется. Например, запись десятичного чис­ла 1998 в римской системе счисления будет выглядеть сле­дующим образом:

MCMXCVIII= 1000+(1000- 100)+(100- 10) +5+ 1+1+1.

Позиционные системы счисления. Первая позиционная система счисления была придумана еще в Древнем Вавило­не, причем вавилонская нумерация была шестидесятерич­ной, то есть в ней использовалось шестьдесят цифр! Инте­ресно, что до сих пор при измерении времени мы используем основание, равное 60 (в 1 минуте содержится 60 секунд, а в 1 часе — 60 минут).

В XIX веке довольно широкое распространение получи­ла двенадцатеричная система счисления. До сих пор мы ча­сто употребляем дюжину (число 12): в сутках две дюжины часов, круг содержит тридцать дюжин градусов и так да­лее. В позиционных системах счисления количествен­ное значение цифры зависит от ее позиции в числе.

Наиболее распространенными в настоящее время позици­онными системами счисления являются десятичная, двоич­ная, восьмеричная и шестнадцатеричная. Каждая позицион­ная система имеет определенный алфавит цифр и основание.

В позиционных системах счисления основание системы равно количеству цифр (знаков в ее ал­фавите) и определяет, во сколько раз различают­ся значения одинаковых цифр, стоящих в сосед­них позициях числа.

Десятичная система счисления имеет алфавит цифр, кото­рый состоит из десяти всем известных, так называемых араб­ских, цифр, и основание, равное 10, двоичная — две цифры и основание 2, восьмеричная — восемь цифр и основание 8, шестнадцатеричная — шестнадцать цифр (в качестве цифр используются и буквы латинского алфавита) и основание 16 (табл. 2.2).

Таблица 1. Позиционные системы счисления

Система счисления	Основание	Алфавит цифр
Десятичная		0,1,2,3,4,5,6,7,8,9
Двоичная		0,1
Восьмеричная		0,1,2,3.4,5,6,7
Шестнадцатеричная		0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А (10). В (11),
		C(12),D(13),E(14),F(15)

Десятичная система счисления. Рассмотрим в качестве примера десятичное число 555. Цифра 5 встречается триж­ды, причем самая правая цифра 5 обозначает пять единиц, вторая справа— пять десятков и, наконец, третья справа — пять сотен.

Позиция цифры_ в числе называется разрядом. Разряд числа возрастает справа налево, от младших разрядов к старшим. В десятичной системе цифра, находящаяся в крайней справа позиции (разряде), обозначает количество единиц, цифра, смещенная на одну позицию влево, — коли­чество десятков, еще левее — сотен, затем тысяч и так да­лее. Соответственно имеем разряд единиц, разряд десятков и так далее.

Число 555 записано в привычной для нас свернутой фор­ме. Мы настолько привыкли к такой форме записи, что уже не замечаем, как в уме умножаем цифры числа на различ­ные степени числа 10.

В развернутой форме записи числа такое умножение за­писывается в явной форме. Так, в развернутой форме запись числа 555 в десятичной системе будет выглядеть следую­щим образом:

Как видно из примера, число в позиционной систем! счисления записывается в виде суммы числового ряда степе ней основания (в данном случае 10), в качестве коэффициентов которых выступают цифры данного числа.

Для записи десятичных дробей используются отрицательные значения степеней основания. Например, число 555,5₁₀ в развернутой форме записывается следующим образом:

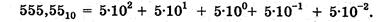
В общем случае в десятичной системе счисления запись числа А, которое содержит п целых разрядов числа и т дробных разрядов числа, выглядит так:

Коэффициенты а в этой записи являются цифрами деся­тичного числа, которое в свернутой форме записывается так:

Из вышеприведенных формул видно, что умножение или деление десятичного числа на 10 (величину основания) при­водит к перемещению запятой, отделяющей целую часть от дробной, на один разряд соответственно вправо или влево. Например:

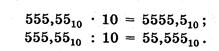
Двоичная система счисления. В двоичной системе счисле­ния основание равно 2, а алфавит состоит из двух цифр (0 и 1). Следовательно, числа в двоичной системе в развернутой форме записываются в виде суммы степеней основания 2 с коэффициентами, в качестве которых выступают цифры О или 1.

Например, развернутая запись двоичного числа может выглядеть так:

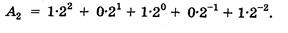
Свернутая форма этого же числа:

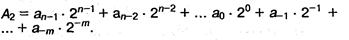
Коэффициенты а. в этой записи являются цифрами (0 или 1) двоичного числа, которое в свернутой форме записывает­ся так:

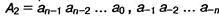
Из вышеприведенных формул видно, что умножение или деление двоичного числа на 2 (величину основания) приво­дит к перемещению запятой, отделяющей целую часть от дробной на один разряд соответственно вправо или влево. Например:.

Позиционные системы счисления с произвольным осно­ванием. Возможно использование множества позиционных систем счисления, основание которых равно или больше 2. В системах счисления с основанием q (q-ичная система счис­ления) числа в развернутой форме записываются в.виде сум­мы степеней основания q с коэффициентами, в качестве ко­торых выступают цифры О, 1, q-1:

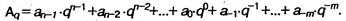
Коэффициенты а. в этой записи являются цифрами числа, записанного в q-ичной системе счисления.

Так, в восьмеричной системе основание равно восьми (q = 8). Тогда записанное в свернутой форме восьмеричное

число А = 673,2₈ в развернутой форме будет^; иметь вид:

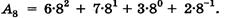
В шестнадцатеричной системе основание равно шестнад­цати (q = 16), тогда записанное в свернутой форме шестнадцатеричное число –A₁₆ = 8A,F₁₆ в развернутой форме будет иметь вид:

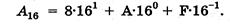
Если выразить шестнадцатеричные цифры через их деся­тичные значения (А=10, F=15), то запись числа примет вид:

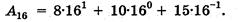
Дата добавления: 2014-01-06