Алгебра высказываний. Алгебра в широком смысле этого слова — наука об общих операциях, аналогичных сложению и умножению, которые мо­гут выполняться над различными математическими

Алгебра в широком смысле этого слова — наука об общих операциях, аналогичных сложению и умножению, которые мо­гут выполняться над различными математическими объектами (алгебра переменных и функций, алгебра векторов, алгебра множеств и так далее). Объектами алгебры логики являются высказывания.

Алгебра логики отвлекается от смысловой содержательности высказываний. Ее интересует только один факт — истинно или ложно данное высказывание, что дает возможность определять истинность или ложность составных высказываний алгебраиче­скими методами.

Простые высказывания в алгебре логики обозначаются за­главными латинскими буквами:

А = {Аристотель — основоположник логики};

В ={На яблонях растут бананы}.

Истинному высказыванию ставится в соответствие 1, ложно­му — 0. Таким образом, А =1, В = 0.

Составные высказывания на естественном языке образуются с помощью союзов, которые в алгебре высказываний заменяют­ся на логические операции. Логические операции задаются таб­лицами истинности и могут быть графически проиллюстриро­ваны с помощью диаграмм Эйлера-Венна.

Логическая операция КОНЪЮНКЦИЯ (логическое умноже­ние):

• в естественном языке соответствует союзу и;

• в алгебре высказываний обозначение &;

• в языках программирования обозначение And.

Конъюнкция — это логическая операция, ставящая в соот­ветствие каждым двум простым высказываниям составное вы­сказывание, являются истинным тогда и только тогда, когда оба исходных высказывания истинны. ⁱ

В алгебре множеств конъюнкции соответствует операция пе­ресечения множеств, то есть множеству, получившемуся в ре­зультате умножения множеств А и В, соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.

Логическая операция ДИЗЪЮНКЦИЯ (логическое сложе­ние):

• в естественном языке соответствует союзу или;

• обозначение у;

• в языках программирования обозначение Or.

Дизъюнкция — это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, ког­да оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно.

В алгебре множеств дизъюнкции соответствует операция объединения множеств, то есть множеству, получившемуся в' результате сложения множеств А и В, соответствует множест­во, состоящее из элементов, принадлежащих либо множеству А, либо множеству В.

Логическая операция ДИВЕРСИЯ (отрицание):

• в естественном языке соответствует словам неверно, что... и частице не;

• обозначение А;

• в языках программирования обозначение Not.

Отрицани е – это логическая операция, которая каждому простому высказыванию ставит в соответствие составное вы­сказывание, заключающееся в том» что исходное высказывание отрицается.;

В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, то есть множеству, получившемуся в результате отрицания множества А, соответствует множество А, дополняющее его до универсаль­ного множества.

Логическая операция ИМПЛИКАЦИЯ (логическое следование):

• в естественном языке соответствует обороту если..., то...;

• обозначением.

Импликация — это логическая операция, ставящая в соот­ветствие каждым двум простым высказываниям составное вы­сказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие.(второе высказывание) ложно.

А	В	A=>B
0	0	1
0	1	1
1	0	0
1	1	1

Логическая операция ЭКВИВАЛЕНЦИЯ (равнозначность):

• в естественном языке соответствует оборотам речи тогда и только тогда; в том и только в том случае;

• обозначения <=>,

Эквиваленция — это логическая операция, ставящая в соот­ветствие каждым двум простым высказываниям составное вы­сказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одно­временно ложны.

Таблица истинности эквиваленции:

А	В	A<=>В
0	0	1
0	1	0
1	0	0
1	1	1

Логические операции имеют следующий приоритет: дейст­вия в скобках, инверсия, &, v, =>, <=>.

Логические выражения и таблицы истинности

Таблицу, показывающую, какие значения принимает со­ставное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказывании, называют таблицей истинности составного высказывания.

Составные высказывания в алгебре логики записываются с помощью логических выражений. Для любого логического вы­ражения достаточно просто построить таблицу истинности.

Алгоритм построения таблицы истинности:

1) подсчитать количество переменных п в логическом выра­жении;

2) определить число строк в таблице, которое равно т = 2";

3) подсчитать количество логических операций в логиче­ском выражении и определить количество столбцов в таблице,

которое равно количеству переменных плюс количество опера­ций;

4) ввести названия столбцов таблицы в соответствии с после­довательностью выполнения логических операций с учетом скобок и приоритетов;

5) заполнить столбцы входных переменных наборами значе­ний;

6) провести заполнение таблицы истинности по Столбцам, выполнен логические операции в соответствии с установленной в п.4 последовательностью.

Пример. Для формулы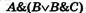построить таблицу истинности алгебраически и с использованием таблиц истинности.

Количество логических переменных 3, следовательно, коли­чество строк в таблице истинности должно быть 2³=8.

Количество логических; операций в формуле 5, следовательно количество столбцов в таблице истинности должно быть 3+5= 8.

Дата добавления: 2014-01-06