Частица в одномерной яме с абсолютно непроницаемыми стенками

В уравнение Шредингера 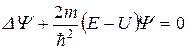полная энергия Е частицы входит в качестве параметра. В теории дифференциальных уравнений доказывается, что уравнения Шредингера удовлетворят стандартным условиям не при любых значениях Е, а лишь при определенных значениях, которые называются собственными значениями энергии (или др. вел.). Решения соот-е собств. зн Е называются собственными функциями. Совокупность собственных значений называется спектром. Спектр бывает дискретным и непрерывным. В случае дискретного спектра собственные значения и собственные функции можно пронумеровать

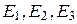
Пусть частица находится между двумя бесконечными стенками, удовлетворяющими условиям

Для одномерного случая уравнение Шредингера

За пределами ямы вероятность обнаружения частицы равна нулю. Следовательно, и . Из условий непрерывности на границах

Для частицы в яме уравнение Шредингера имеет вид

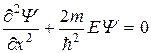
Обозначим . Для уравнения общим решением является

Из условия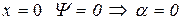

Из условия

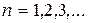
При то есть частица отсутствует.

Откуда

Выразив из энергию, получим:

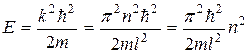
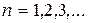
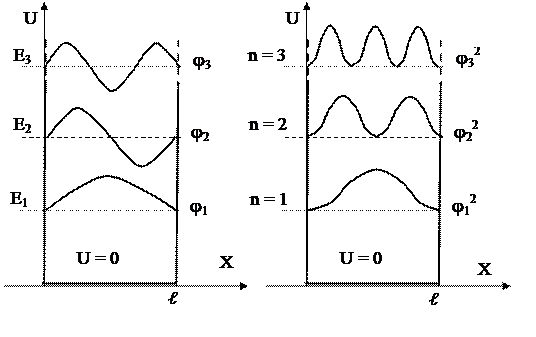Спектр энергии дискретный. Если посчитать разницу между соседними уровнями энергии и в качестве частицы взять молекулу 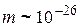кг, то для ширины ямы ~ 10 см получим 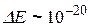эВ. То есть, чем больше m и больше l, тем гуще уровни энергии. Для электрона и l ~ 10^-10 м (атомн. размеры) 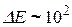эВ.

Найдем собственные функции

Для нахождения А воспользуемся условием нормировки

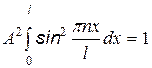
Функция на концах промежутка х = 0 и x = l обращается в ноль, поэтому интеграл можно получить, умножив среднее значение 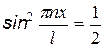на l.

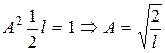
Откуда

В состоянии n = z вероятность частицы нахождения посередине ямы рана 0. Классическая физика – все положения равновероятны.

ЛЕКЦИЯ № 10

Дата добавления: 2014-01-06