Структурные средние

Структурные средние применяются для изучения внутреннего строения и структуры рядов распределения значений признака.

В качестве структурных средних чаще всего используют показатели моды и медианы.

1. Мода – наиболее часто повторяющееся значение признака в изучаемой совокупности.

Для дискретных рядов распределения модой будет то значение признака, у которого наибольший удельный вес. В интервальных рядах распределения с равными интервалами мода определяется по формуле:

Мо = ,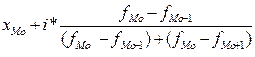

где 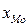- начальное значение интервала, содержащего моду;

i – величина модального интервала;

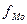- частота модального интервала (в абсолютном или относительном выражении);

- частота интервала, предшествующего модальному;

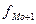- частота интервала, следующего за модальным.

Мода широко применяется в коммерческой деятельности.

2. Медиана – величина признака, которая делит упорядоченную последовательность его значений на 2 равные по численности части.

Если ряд распределения дискретный и имеет нечетное число значений, то медианой будет значение признака, находящееся в середине упорядоченного ряда. Например, стаж пяти рабочих составил 2, 4, 7, 8 и 10 лет. В таком упорядоченном ряду медиана – 7 лет.

Если упорядоченный ряд состоит из четного числа значений, то медианой будет средняя арифметическая из 2 значений признака, расположенных в середине ряда. Пусть в бригаде не 5 человек, а 6, имеющих стаж работы 2, 4, 6, 7, 8 и 10 лет. В центре ряда стоят 6 и 7, т. е. средняя арифметическая этих значений и будет медианой ряда: Ме = (6+7)/2=6,5 лет.

В интервальном вариационном ряду медиана определяется по формуле:

,

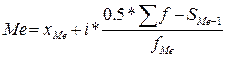где 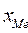- начальное значение интервала, содержащего медиану;

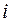- величина медианного интервала;

- сумма частот ряда;

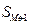- сумма накопленных частот, предшествующих медианному интервалу;

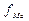- частота медианного интервала.

Нахождение медианы в интервальных вариационных рядах требует предварительного определения интервала, в котором находится медиана, т.е. медианного интервала – этот интервал характеризуется тем, что его кумулятивная частота равна полусумме или превышает полусумму всех частот ряда.

Медиана используется при контроле качества продукции и технологического процесса на промышленных предприятиях, а также при изучении распределения домохозяйств по величине дохода.

Мода и медиана являются дополнительными к средней величине характеристиками совокупности и используются в статистике для анализа формы рядов распределения.

Если значение средней величины совпадает с модой и медианой, то ряд является симметричным. На практике строго симметричные ряды встречаются довольно редко, чаще исследователю приходится иметь дело с асимметричными рядами. Простейшим показателем асимметрии может служить разность между средней арифметической величиной и модой.

Если A_S = 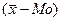<0, то в ряду имеет место левосторонняя асимметрия, если A_S = 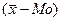>0, то – правосторонняя.

К структурным характеристикам исследуемой совокупности относятся также:

- квартили, делящие совокупность на 4 равные части,

- квинтили, делящие совокупность на 5 равных частей;

- децили, делящие совокупность на 10 частей,

- перцентили, делящие совокупность на 100 частей.

Вопросы для самоконтроля

1. Что такое статистический показатель? Какие виды статистических показателей Вы знаете?

2. Каково значение абсолютных величин в статистике? В каких единицах они измеряются? Приведите примеры.

3. Что характеризуют относительные статистические показатели? На какие виды они делятся?

4. Дайте определение средней величины.

5. Какие виды средних величин применяются в статистике?

6. В каких случаях применяются степенные средние?

7. Какие свойства средней арифметической Вы знаете?

8. Для чего используются структурные средние? На какие виды они подразделяются?

Глава 4. Вариация признака

Цель: усвоить и закрепить материал по теме, научиться проводить анализ вариационных рядов.

Дата добавления: 2014-01-06