
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Временные режимы работы реактора
|
|
|
|
Временные режимы работы: подкритический, критический, надкритический. Временной режим реактора при работе на мощности. Средства управления реактором – органы регулирования. Долговременные процессы в реакторе. Выгорание топлива. Эффекты отравления.
Подкритический режим. Рассмотрим подкритическую систему с k<1, внутри которой расположен постоянно действующий источник быстрых нейтронов мощностью Q (н/с). При расчете пследующих друг за другом актов цепной реакции получаем сходящийся ряд, сумма которого 1/(1-k), который называется подкритическим коэффициентом размножения. При k=0,99 подкритический коэффициент размножения равен 100.
Надкритический режим. Рассмотрим надкритическую систему и проанализируем скорость изменения в нем количества нейтронов. Если в некоторый момент времени в реакторе имеется n нейтронов, то по определению коэффициента размножения их число по прошествию одного цикла обращения станет равным kn, где k – коэффициент размножения нейтронов. А приращение нейтронов за время цикла составит kn-n=n(k-1). Следовательно изменение числа нейтронов во времени описывается уравнением:
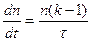 (7.1)
(7.1)
Решение этого уравнения дает зависимость числа нейтронов в реакторе от времени:
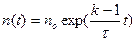 , (7.2)
, (7.2)
где no – число нейтронов в реакторе в начальный момент.
Наибольшее время цикла мгновенных нейтронов деления в реакторе на тепловых нейтронах достигает 10-3 с. Если предположить, что k=1,01, то через каждую секунду число нейтронов в реакторе возрастает в е10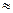 20000 раз и в такое же число раз возрастет число делений в реакторе. В средах с большим содержанием делящихся материалов время нейтронного цикла уменьшается и для чистых делящихся материалов может достигать 10-8 с. В последнем случае при k=1,1 один начальный нейтрон через 6 мкс порождает 1026 нейтронов, а одно деление – порождает 1026 делений, что эквивалентно делению около 40 кг урана.
20000 раз и в такое же число раз возрастет число делений в реакторе. В средах с большим содержанием делящихся материалов время нейтронного цикла уменьшается и для чистых делящихся материалов может достигать 10-8 с. В последнем случае при k=1,1 один начальный нейтрон через 6 мкс порождает 1026 нейтронов, а одно деление – порождает 1026 делений, что эквивалентно делению около 40 кг урана.
Управление надкритическим реактором при таких параметрах изменения потока нейтронов практически невозможно, имея ввиду необходимость механических перемещений элементов системы управления и защиты (СУЗ) реактора. Наличие запаздывающих нейтронов позволяет решить эту проблему, благодаря тому, что периоды полураспада радионуклидов, в результате распада которых они испускаются, составляют от долей секунды до 56 секунд. Рассмотрим особенности изменения мощности реактора (плотности потока нейтронов) при наличии запаздывающих нейтронов.
Итак скорость возрастания числа нейтронов со временем определяется превышением коэффициента размножения k над единицей и временем нейтронного цикла τ (см. соотношение 7.2). Для мгновенных и запаздывающих нейтронов времена нейтронных циклов существенно отличаются. Хотя доля запаздывающих нейтронов невелика, они могут дать существенный вклад в усредненное по всем нейтронам время цикла. В самом деле, в точно критическом реакторе (k=1) β -ая часть нейтронов деления имеет время цикла обращения, определяемое средним временем жизни радиоактивных продуктов деления, являющихся предшественниками запаздывающих нейтронов, и равное τз. Оставшаяся часть нейтронов (1-β) имеет время цикла мгновенных нейтронов τм. Поэтому, с учетом выходов каждой составляющей среднее время цикла равно:
τ = (1-β) τм + βτз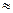 βτз (6.4)
βτз (6.4)
Продукты деления 235U имеют βτз =0,085 с, что во много раз больше τм даже в реакторе на тепловых нейтронов, где время цикла свободного нейтрона особенно велико и достигает 10-3 с. Это позволяет значительно снизить скорость нарастания потока нейтронов в надкритическом состоянии. Время среднего цикла, вычисляемого по соотношению (6.4) относится к точно критическому реактору. Значительное превышение k над единицей приводит к снижению эффективной доли запаздывающих нейтронов, при этом τ приближается к τм при 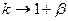 . Однако в некотором легко контролируемом интервале изменения k τ остается много больше τм, что и используется при управлении цепной реакцией с помощью запаздывающих нейтронов.
. Однако в некотором легко контролируемом интервале изменения k τ остается много больше τм, что и используется при управлении цепной реакцией с помощью запаздывающих нейтронов.
Величина
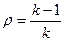 (6.5)
(6.5)
называется реактивностью ядерного реактора.
Понятие реактивности широко используется при управлении ядерного реактора. Поскольку при управлении реактором величина k мало отличается от единицы, то 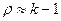 , т.е. реактивность показывает превышение коэффициента размножения k над единицей. В критическом реакторе ρ=0, в надкритическом реакторе реактивность положительна, а в подкритическом – отрицательна.
, т.е. реактивность показывает превышение коэффициента размножения k над единицей. В критическом реакторе ρ=0, в надкритическом реакторе реактивность положительна, а в подкритическом – отрицательна.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 405; Нарушение авторских прав?; Мы поможем в написании вашей работы!