Расчет витков крепежных и ходовых резьб

Лекция 5

Условие самоторможения винтовой пары.

При отвинчивании гайки окружная сила и сила трения меняют направление. Поэтому окружная сила равна

F_t = F∙tg (ρ¹-φ).

Момент отвинчивания в резьбе без учета трения на торце гайки определится

F_отв = F∙tg (ρ¹-φ)/2

Самоторможение будет, если Т_отв>0; tg (ρ¹-φ)>0; p¹>φ.

Для крепежных резьб значение угла подъема лежит в пределах 2,5°...3,5°, а угол трения изменяется в зависимости от коэффициента трения в пределах 6°...16°. Поэтому все крепежные резьбы - самотормозящие при статических нагрузках. Однако при вибрациях коэффициент трения существенно снижается и условие самоторможения нарушается. Поэтому при переменных нагрузках необходимы специальные средства стопорения резьбовых соединений.

Основным видом разрушения крепежных резьб является срез витков. Причем, если материалы болта и гайки одинаковы, то опасен срез витков болта, происходящей по цилиндрической поверхности диаметра d₁. Напряжение среза в резьбе болта:

τ₁=F_x/πd₁∙H∙K∙K_m ≤[τ₁]

а в резьбе гайки

τ₂=F_x/πd∙H∙K∙K_m ≤[τ₂].

Здесь Н -высота гайки (или глубина завинчивания винта);

К -коэффициент полноты резьбы;

К_m -коэффициент неравномерности нагрузки по виткам резьбы.

Рисунок 6

Напряжения смятия в резьбе:

σ=4F_x/[(d²-d₁²)∙z∙K_m] ≤[s_см ],

z = Н/р,

где р - шаг резьбы,

z-число рабочих витков гайки.

Равнопрочность резьбы и стержня болта является одним из условий назначения стандартных параметров резьбовых деталей (в частности, высоты стандартных гаек, головок болтов, диаметров гаек и т.д.). Поэтому при прочностных расчетах стандартных резьбовых деталей элементы резьбы не рассчитываются, а прочность определяется по прочности стержня болта.

При проектировании резьбовых соединений рассматриваются следующие случаи нагружения.

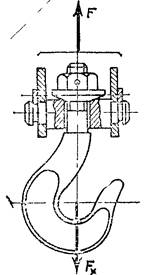Случай 1. Незатянутое резьбовое соединение, нагруженное осевой растягивающей силой.

Рисунок 7

Стержень болта под действием осевой силы может разрушиться. Опасным является сечение, ослабленное резьбой. Площадь этого сечения оценивают приближенно по внутреннему диаметру резьбы. Условие прочности по напряжениям растяжения в стержне:

σ=F_x/(πd₁²/4)≤[σ]

Для проектировочного расчета получим:

Диаметры резьбы округляют до стандартного значения.

Случай 2. Винт нагружен осевой растягивающей силой и может подтягиваться под нагрузкой.

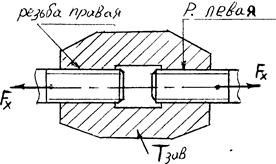Рисунок 8

Вэтом случае стержень болта растягивается осевой силой, возникающей от затяжки болта, и закручивается моментом сил в резьбе. Нап­ряжения растяжения от силы затяжки:

s_р=4∙F/πd₁².

Напряжения кручения от момента в резьбе:

t_кр =T_p/W_p=0,5F_зат∙d₂∙tg(φ+ρ¹)/0,2d₁³.

Прочность болта определяют по эквивалентному напряжению:

Вычисления показывают, что для стандартных резьб σ_экв=1,3σ. Это позволяет рассчитывать прочность болтов по упрощенной формуле:

σ_экв=1,3F_зат/(πd₁²/4).

Тогда для проектировочного расчета

Случай 3. Болтовое соединение нагружено силами, сдвигающими детали в стыке. Рассмотрим данный случай более подробно.

Дата добавления: 2014-01-06