
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 11. Физика Вселенной
|
|
|
|
Статистическое описание поведения одной частицы из ансамбля осуществляется посредством функции, которую называют плотностью вероятности нахождения частицы в данной точке в данный момент.
Это соотношение называется условием нормировки.
Функции, удовлетворяющие этому условию, называются нормированными.
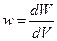 .
.
Из условия нормировки вытекает, что квадрат модуля волновой функции дает плотность вероятности нахождения частицы в соответствующем месте в данный момент времени.
Из физического смысла волновой функции вытекают стандартные условия, накладываемые на нее:
1. 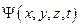 должна быть однозначной, непрерывной и конечной во всех точках пространства (кроме особых точек).
должна быть однозначной, непрерывной и конечной во всех точках пространства (кроме особых точек).
2. Производная от волновой функции 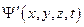 тоже должна быть непрерывной и конечной во всех точках пространства.
тоже должна быть непрерывной и конечной во всех точках пространства.
Из физического смысла волновой функции следует, что квантовая механика имеет статистический характер. Она не позволяет определить точное местонахождение микрочастицы или ее траекторию. С помощью волновой функции можно лишь предсказать, с какой вероятностью частица может быть обнаружена в различных точках пространства.
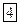 В развитие идей де Бройля о волновых свойствах материи австрийский физик Шрёдингер в 1926 году получил уравнение, которое позволяет найти волновые функции частиц, движущихся в различных силовых полях.
В развитие идей де Бройля о волновых свойствах материи австрийский физик Шрёдингер в 1926 году получил уравнение, которое позволяет найти волновые функции частиц, движущихся в различных силовых полях.
Шрёдингер вывел свое уравнение исходя из оптико-механических аналогий, которые заключаются в сходстве уравнений, описывающих ход светового луча с уравнениями, определяющими траектории движения частиц в классической механике.
Это уравнение является основным уравнением нерелятивистской квантовой механики. Оно не может быть получено из других соотношений и его справедливость доказывается тем, что все вытекающие из него следствия самым точным образом согласуются с опытными данными.
Для свободно двигающейся частицы (нет силового поля) уравнение Шрёдингера имеет вид:
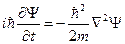 ,
,
где  - оператор Лапласа.
- оператор Лапласа.
Если частица двигается в потенциальном поле, то уравнение Шрёдингера имеет вид:
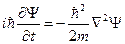
 ,
,
где U- потенциальная энергия частицы.
В теории дифференциальных уравнений доказывается, что уравнения вида:
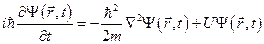 ,
,
имеют решения, удовлетворяющие стандартным условиям лишь при некоторых избранных значениях энергии, которые называются собственными.
Совокупность собственных значений энергии называется спектром этой величины.
Если средние значения всех физических величин, характеризующих состояние микрочастицы, не зависят от времени, состояние называется стационарным, и оно описывается функцией вида:
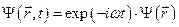 .
.
Уравнение Шрёдингера для стационарных состояний имеет вид:
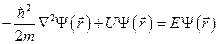 ,
,
или 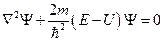 .
.
В дальнейшем мы будем иметь дело только с такими уравнениями, называя их просто уравнениями Шрёдингера.
Решения этого уравнения образуют дискретный энергетический спектр, определяемый номером состояния n, каждое из этих состояний является стационарным.
Основным состоянием называется состояние, описываемое волновой функцией, которая соответствует наименьшему значению энергии Е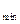 .
.
Иногда одному и тому же значению энергии Е соответствует несколько различных состояний частицы. Такие состояния называются вырожденными, а их число называют кратностью вырождения.
ЛЕКЦИЯ 4
ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ (продолжение)
5. Частица в одномерной потенциальной яме.
6. Частица в ящике с непроницаемыми стенками.
7. Гармонический осциллятор.
8. Прохождение частицы через потенциальный барьер. Туннельный эффект.
 Пусть некоторая частица находится в одномерной потенциальной яме шириной
Пусть некоторая частица находится в одномерной потенциальной яме шириной  с бесконечно высокими стенками. В такой яме частица может перемещаться только вдоль оси ОХ, следовательно
с бесконечно высокими стенками. В такой яме частица может перемещаться только вдоль оси ОХ, следовательно  .
.
Между стенками ямы потенциальная энергия частицы равна нулю, т.е. при 0< U=0; за стенками ямы эта энергия бесконечно велика, т.е. при
U=0; за стенками ямы эта энергия бесконечно велика, т.е. при 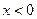 и
и 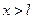
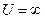 .
.
Определим возможные значения энергии, выражения для собственных волновых функций частицы и распределение вероятности нахождения её по ширине потенциальной ямы.
Уравнение Шрёдингера в данном случае будет иметь вид:
 .
.
Рис. 14.
Обозначив  , получим:
, получим:  .
.
Уравнение по виду аналогично уравнению свободных незатухающих колебаний, но переменной в нем является координата, так как стационарные состояния от времени не зависят.
Граничные условия и условие непрерывности волновой функции позволяют записать:
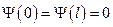 .
.
Решение данного уравнения будем искать в виде: 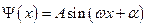 .
.
Из граничных условий следует, что:
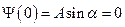 ,
, 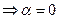 ;
;
 ,
, 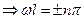 ,
,  ,
,
где n=1,2,3,…, но не равно нулю, так как в этом случае  при любых х.
при любых х.
А это означает, что частицы в яме нет.
Получили, что  , откуда
, откуда 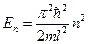 .
. 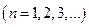
То есть, частица в потенциальной яме может принимать дискретный ряд разрешенных значений, определяемых этим условием.
Теперь найдем собственные значения волновой функции.
Поскольку энергетический спектр является дискретным, следовательно, и значения волновой функции будут тоже образовывать дискретный ряд:
 .
.
Амплитуду волновой функции найдем из условия нормировки:
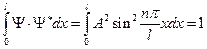 .
.
Воспользовавшись теоремой о среднем  , получим:
, получим:  ,
,
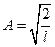 .
.
Окончательно собственные значения волновой функции для данного случая можно записать:
 .
.
Плотность вероятности обнаружения частицы в состояниях, описываемых найденной
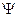 -функцией, по определению равна:
-функцией, по определению равна:
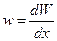
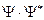
 .
.
Пусть n =1, тогда учитывая, что 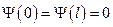 вероятность обнаружить частицу на краях ямы практически равна нулю; при
вероятность обнаружить частицу на краях ямы практически равна нулю; при 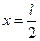 функция
функция 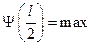 .
.
То есть, вероятность обнаружить частицу максимальна в центре ямы и убывает по синусоиде к её краям.
Пусть n =2, тогда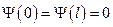 и
и  ,
, 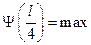 и
и  .
.
Отсюда следует, что максимальная вероятность обнаружить частицу соответствует двум точкам одновременно, что противоречит классическим представлениям.
Графики изменения значений энергий, волновых функций и распределения плотностей вероятности по ширине ямы при различных n приведены на рис.15.
Рис.15
 Рассмотрим в рамках квантовой механики движение частицы в ограниченном пространстве, которое имеет форму прямоугольного параллелепипеда (потенциальный ящик).
Рассмотрим в рамках квантовой механики движение частицы в ограниченном пространстве, которое имеет форму прямоугольного параллелепипеда (потенциальный ящик).
Уравнения плоскостей, ограничивающих данный объём, имеют вид:

Будем считать, что частица движется свободно только внутри рассматриваемого объёма, а вне него её потенциальная энергия бесконечно велика.
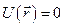 при
при 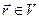 ; и
; и  при
при 
Согласно граничным условиям, волновая функция, описывающая состояние частицы, вне потенциального ящика всюду равна нулю.
Внутри него волновая функция может быть найдена по уравнению Шрёдингера:

На стенках ящика, в силу условия непрерывности, волновая функция должна быть равна нулю.
Стационарные состояния частицы в ящике будут описываться волновой функцией вида:
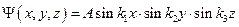 ,
,
где 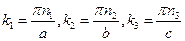


То есть совокупность чисел  можно рассматривать как трехзначный номер волновой функции.
можно рассматривать как трехзначный номер волновой функции.
Подстановка полученной волновой функции в уравнение Шрёдингера показывает, что она является его решением, если:
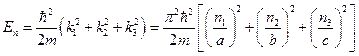 .
.
Величины  можно рассматривать как проекции волнового вектора
можно рассматривать как проекции волнового вектора 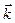 на оси координат, тогда:
на оси координат, тогда:  .
.  .
.
Постоянную А находим из условия нормировки:
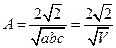 .
.
Окончательно получим, что волновая функция, описывающая состояния частицы в потенциальном ящике, образует счетное множество и имеет вид:
 .
.
Соответствующие этим состояния энергии образуют дискретный спектр.
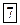 Гармоническим осциллятором называют частицу массой m, совершающую одномерное колебательное движение под действием квазиупругой (упругой) силы, подчиняющейся закону:
Гармоническим осциллятором называют частицу массой m, совершающую одномерное колебательное движение под действием квазиупругой (упругой) силы, подчиняющейся закону:
 .
.
Потенциальная энергия такой частицы равна:
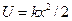 .
.
Учитывая, что  , потенциальную энергию можно представить в виде:
, потенциальную энергию можно представить в виде:
 .
.
Поскольку движение одномерное, то оператор Лапласа будет иметь вид:  , и тогда уравнение Шрёдингера, описывающее движение гармонического осциллятора можно записать:
, и тогда уравнение Шрёдингера, описывающее движение гармонического осциллятора можно записать:
 , где Е – полная энергия осциллятора.
, где Е – полная энергия осциллятора.
В теории дифференциальных уравнений доказывается, что это уравнение имеет конечные, однозначные и непрерывные решения при:
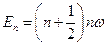 , где n = 0,1,2,3….
, где n = 0,1,2,3….
Следовательно, гармонический осциллятор также имеет дискретный спектр энергетических уровней, которые являются эквидистантными (отстоят друг от друга на одинаковом расстоянии).
Рис.16
Наименьшее возможное значение энергии осциллятора равное  называется нулевой энергией.
называется нулевой энергией.
Существование нулевой энергии у квантового осциллятора вытекает из принципа неопределенности.
Согласно классической теории полная энергия осциллятора равна:
 .
.
Поскольку у квантового осциллятора импульс и координата не могут одновременно определенные значения, то и равны нулю одновременно они не могут быть.
Существование нулевой энергии подтверждается экспериментами по изучению рассеяния света на кристаллах при низких температурах. Оказалось, что интенсивность рассеянного света по мере понижения температуры стремится не к нулю, а к некоторому конечному значению, что указывает на то, что при абсолютном нуле колебания атомов в кристаллической решетке не прекращаются.
Квантовая механика позволяет вычислить вероятность переходов квантовой системы из одного состояния в другое. Подобные вычисления для квантового осциллятора показали, что для него возможны переходы только между соседними уровнями, отстоящими друг от друга на  .
.
При таких переходах квантовое число n меняется на единицу,  .
.
Условия, накладываемые на изменение квантовых чисел при переходах из одного состояния в другое называются правилами отбора.
Таким образом, квантовая механика достаточно строго доказала, что атомы (а именно они являются квантовыми осцилляторами) излучают энергию порциями, величина которых равна  . Этот результат Планк в своё время вынужден был постулировать.
. Этот результат Планк в своё время вынужден был постулировать.

К настоящему времени сложились определенные научные представления о происхождении и эволюции Вселенной. Одним из основных затруднений при изучении астрономических и космологических явлений и объектов является то, что над ними нельзя провести контрольных экспериментов. Можно наблюдать лишь естественный ход событий. Поэтому поразительным является не безграничное разнообразие наблюдаемых астрономических событий, а возможность, анализируя эти явления, делать выводы относительно эволюции звезд и галактик на протяжении миллиардов лет.
Остановимся на физических основаниях космологии и астрофизики. Предметом космологии является изучение строения, происхождения и эволюции Вселенной как целого. Поэтому космология связана с общей теорией относительности (ОТО), поскольку во Вселенной приходится иметь дело с огромными расстояниями, скоростями и огромными массами.
1. Космологическая модель А. Эйнштейна – А.А. Фридмана
Первая современная космологическая теория была предложена Эйнштейном в 1917 г. в качестве следствия его формулировки ОТО. Эйнштейн показал, что ОТО однозначно объясняет возможность существования статической Вселенной, которая не изменяется со временем. Как мы сейчас понимаем, этого не может быть, но в то время казалось, что это важный успех ОТО. Этот парадокс, по-видимому, был связан с тем, что еще из представлений ученых Древней Греции и Египта утвердилось мнение о незыблемости, стационарности Вселенной, и модель Эйнштейна как будто подтвердила это. Однако уже в 1922 г. А. Фридман показал, что из самих уравнений общей теории относительности следует нестационарность, т.е. развитие Вселенной.
Обосновывая в 1917 г. ОТО, А. Эйнштейн ввел понятие космологического члена λ, (постоянной) как раз для обоснования статичности его модели Вселенной, о чем, я думаю не без влияния А. Фридмана, в 1923 г. писал: «Прочь космологическую постоянную!» По свидетельству Г. Гамова А. Эйнштейн считал «введение космологической постоянной самой грубой ошибкой своей жизни».
Космологическая постоянная была не чем иным, как приемом, который студент-первокурсник назвал бы «коэффициент вранья» – абсолютно субъективной подгонкой к тому объективному решению, которое ему хочется получить. Этот «коэффициент» позволил его уравнениям дать желаемый А. Эйнштейну результат.
А. Фридман утверждал, что искривленное пространство не должно быть стационарным, оно должно или расширяться, или сжиматься. И Эйнштейн вынужден был публично согласиться с выводами Фридмана.
К сожалению, работы Фридмана, в частности его книга «Мир как пространство и время», умалчивались вплоть до последнего времени, а автором теории расширяющейся Вселенной объявили аббата Ж. Леметра, президента папской академии наук в Ватикане. В значительной мере это связано с идеологической компанией, развернутой в СССР в 30–50-е годы. Стационарная, бесконечная в пространстве и времени Вселенная фигурировала и в философии Канта, Гегеля и Энгельса и была «узаконена» марксистско-ленинской философией. Все другие представления были объявлены ошибочными и лженаучными, в том числе и сама ОТО Эйнштейна.
Через какое-то время теория расширяющейся Вселенной была подтверждена экспериментально. Из оптических наблюдений звезд было установлено, что кроме нашей Галактики, звездного скопления в виде Млечного пути, существует огромное количество других галактик. По смещению световых лучей к красному концу видимого спектра можно определить скорость движения объекта относительно наблюдателя. В более общем виде – это так называемый эффект Доплера при распространении волны любой природы и движении источника этой волны относительно наблюдателя. Например, звуковой сигнал движущегося поезда относительно неподвижного наблюдателя на платформе будет выше, когда поезд приближается к нам. И ниже, когда он от нас удаляется. С помощью эффекта Доплера экспериментально наблюдали и измеряли радиальные движения (от нас или к нам) отдельных звезд, а затем и галактик. Было установлено, что если звезда движется к нам, то спектральные линии смещаются к фиолетовому концу спектра, если от нас – то к красному концу.
При анализе изучения далеких галактик получили удивительный результат: у всех галактик наблюдали красное смещение! Поэтому можно считать, что они удаляются от нас. Причем величина этого красного смещения и, следовательно, скорость разбегания галактик – больше для более удаленных галактик (что само по себе чрезвычайно удивительно, и до сих пор причина этого не выяснена). Американский астроном Э. Хаббл (1889–1953) установил в 1929 г. закон.
Этот закон экспериментально подтвердил расширение Вселенной. Из него можно определить возраст Вселенной, который оценивается в 10–20 миллиардов лет. По данным радиоактивного распада некоторых веществ возраст Земли определяется в 5 миллиардов лет.
Если все галактики удаляются от нас, то возникает вопрос: не занимаем ли мы особого положения во Вселенной? Простой физический опыт не дает оснований полагать, что это так. Предположим, что мы надуваем воздушный шарик, на поверхности которого равномерно нанесены пятнышки. По мере того как шарик будет раздуваться, наблюдателю, находящемуся на одном из пятнышек, будет казаться, что все другие пятнышки удаляются от него. Более того, ему будет казаться, что более далекие пятнышки удаляются значительно быстрее, чем те, которые расположены близко. Такие же результаты получаются, естественно, при наблюдении с любого другого пятнышка.
Таким образом, при однородном расширении будут увеличиваться все расстояния между пятнышками. Поэтому измерение красного смещения обычно трактуется как очевидное доказательство того, что Вселенная расширяется. Так как расширение, по-видимому, происходит равномерно во все стороны, то «центра» Вселенной явно выделить нельзя. Естественно, остается много вопросов: почему Вселенная расширяется, будет ли она расширяться дальше или сожмется? Конечна она или бесконечна? Как образуются галактики, из чего состоят? и т.д.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 437; Нарушение авторских прав?; Мы поможем в написании вашей работы!