Затем из каждого оставшегося уравнения вида

()

вычитается полученное уравнение (3), умноженное на коэффициент a_i1. В итоге, после выполнения первого шага прямого хода система уравнений примет следующий вид

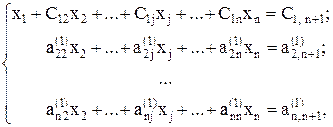(4)

где

На втором шаге указанные выше действия повторяются над (n - 1) уравнениями системы (4), всеми кроме первого, с целью исключения переменной x₂, где .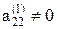

В итоге получим

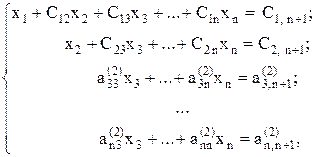
где

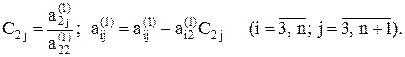
Повторяя шаги прямого хода (n - 1) раз, окончательно получим систему уравнений треугольного вида

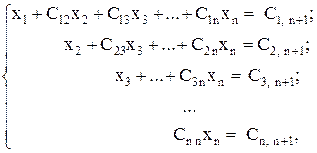(5)

где

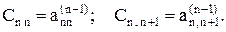
При программной реализации прямого хода используется расширенная матрица коэффициентов A¢

,

для которой элементы имеют следующий смысл

1) - начальные значения;

2) 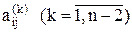- промежуточные значения;

3) 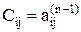- конечные значения.

Для определения элементов матрицы A¢ на некотором k-ом шаге

()

используются следующие расчетные формулы

Обратный ход метода Гаусса. После приведения исходной системы уравнений (1) к треугольному виду (5) вычисляются значения корней по следующим формулам

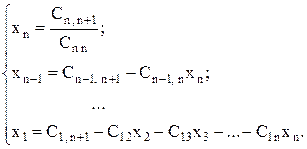
Таким образом, расчетные формулы обратного хода имеют вид

6. Итерационные методы

При решении систем уравнений высокого порядка с разреженными матрицами коэффициентов, которые характерны для большинства задач автоматизации проектирования сложных систем, наиболее эффективно применение итерационных методов. Такие методы (например, последовательных приближений и Зейделя) позволяют получать значения корней системы с заданной точностью в виде последовательности

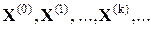некоторых векторов, сходящихся к точному решению X*. Эффективность применения итерационных методов зависит от удачного выбора начального приближения и скорости сходимости процесса вычислений.

Итерационные методы используют особенности разреженных матриц коэффициентов, поскольку ненулевые элементы вычисляются по специальным выражениям по мере необходимости. Поэтому для их реализации требуется меньшее количество вычислительных операций (около n²) и соответствующих затрат машинного времени. Важным преимуществом итерационных методов также является несущественное влияние погрешностей вычислений, так как любое ошибочное приближение может рассматриваться как новый начальный вектор.

Метод последовательных приближений Якоби (итераций). Пусть дана система линейных уравнений, для которой диагональные элементы

.

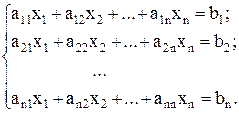
Тогда переменную x₁ можно выразить через первое уравнение, 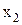- через второе уравнение и т. д.

(10)

где и

Система (10) называется системой линейных уравнений, приведенной к нормальному виду. Матричная форма записи такой системы представляется как

(11)

где

При решении системы (11) за нулевое приближение корней может быть принят столбец свободных членов, т.е. 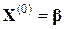. Любое k-е приближение (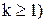вычисляется по формуле

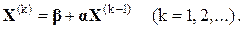
Если последовательность приближений ,,,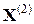..., ,... имеет предел , то этот предел является точным решением 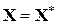системы уравнений (2). Итерационная формула, которая может использоваться при программировании метода Якоби, представляется в обозначениях исходной системы (1) следующим образом

Вычисления продолжаются до тех пор, пока значения не станут достаточно близкими к 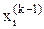для всех 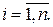Формальное условие прекращения итерационного процесса записывается как

(12)

где e - некоторое заданное положительное число, характеризующее точность (погрешность) определения корней системы уравнений.

Метод Зейделя

Метод Зейделя представляет собой модификацию метода последовательных приближений. При определении значения переменной на некоторой (k+1)-й итерации используются уже вычисленные (k+1)-е приближения неизвестных 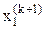, ,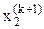..., , 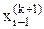а также значения 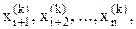полученные на предыдущей k-й итерации.

Пусть дана линейная система уравнений (10). Выбранные начальные приближения корней 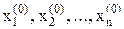подставляются в первое уравнение

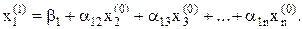
Для определения полученное значение 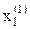сразу же подставляется во второе уравнение системы

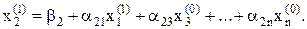
Аналогично определяются приближения корней . Значение 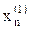вычисляется с использованием первых приближений всех переменных как

В общем случае получение значений неизвестных по методу Зейделя на некоторой k-ой итерации производится по следующей формуле

При использовании обозначений исходной системы уравнений (1) итерационная формула обычно записывается как

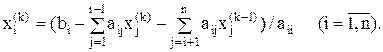
Условие завершения итерационного процесса по методу Зейделя также формулируется в виде соотношения (12). При этом, как правило, процесс сходится к единственному решению быстрее, чем при использовании метода последовательных приближений Якоби.

Условия сходимости итерационных процессов. Пусть дана приведенная к нормальному виду система (11) линейных уравнений. Итерационные процессы последовательных приближений и Зейделя для системы (11) сходятся к единственному решению независимо от выбора начального приближения, если выполняется хотя бы одно из следующих условий

Приведенные соотношения означают, что сумма модулей элементов любой строки или любого столбца матрицы a должна быть меньше единицы.

Таким образом, для сходимости указанных итерационных процессов достаточно, чтобы значения элементов a_ij матрицы a при i ¹ j были небольшими по абсолютной величине. Можно показать, что для линейной системы вида (2) итерационные процессы последовательных приближений и Зейделя сходятся к точному решению X^*, если для всех уравнений системы модули диагональных коэффициентов исходной системы удовлетворяют условиям

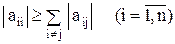
и по крайней мере для одного из уравнений выполняется соотношение

Линейную систему (2) можно заменить такой эквивалентной системой нормального вида (11), которая удовлетворяет условиям сходимости итерационных процессов. Для этого используются следующие элементарные преобразования:

1) перестановка двух строк или столбцов;

2) умножение всех элементов какой-либо строки на одно и то же число, отличное от нуля;

3) сложение элементов какой-либо строки с соответствующими элементами другой строки, умноженными на одно и то же число.

Это исходная система

Модули диагональных элементов в первых двух строках меньше суммы модулей остальных элементов строк. Условие сходимости не обеспечено. Но если поменять эти строки местами диагональные элементы станут преобладающими (не забудем поменять местами соответствующие свободные члены).

Преобразуем систему к итерационному виду

x=b+ax

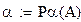
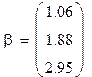
Корни методами итераций и Зейделя

Как и ожидалось у метода Зейделя более высокая скорость сходимости

Используемые процедуры

Процедура метода итераций (Якоби)

Процедура метода Зейделя

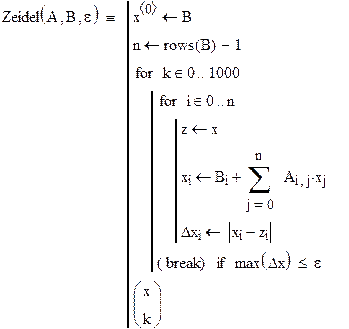
Процедура получения матрицы a

Процедура получения вектора b

Дата добавления: 2014-01-06