
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение систем нелинейных уравнений методом Ньютона
|
|
|
|
Пример
Дана система нелинейных уравнений:

Необходимо определить область сходимости системы, выбрать начальную точку и найти одно из решений системы.

Преобразуем систему для решения методом итераций

Проверяем условие сходимости (10.4). Для заданной системы оно имеет вид:

Находим:
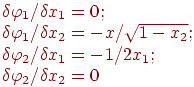
В результате условие (10.4) будет иметь вид:

Определяем область сходимости G.
Граница области сходимости определится при решении системы,

Отсюда х1=0,5;  .
.
В результате область сходимости определится при  и
и .
.
На графике уравнений строим область сходимости G:
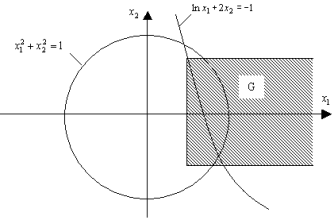
Для обеспечения сходимости в общем случае рекомендуется функцию из (3.5) искать в виде
из (3.5) искать в виде

| (3.7) |
Здесь  ,
,
где 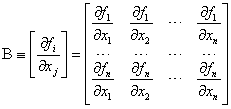 - матрица Якоби - матрица Якоби
| (3.8) |
Будем предполагать, что матрица – неособенная. Подставив выражение
– неособенная. Подставив выражение из формулы (3.7) в (3.5), запишем следующую итерационную формулу:
из формулы (3.7) в (3.5), запишем следующую итерационную формулу:

| (3.9) |
Приведём запись этой формулы для соответствующих компонент вектора  :
:

| (3.10) |
 – элементы матрицы
– элементы матрицы .
.

Модификацией метода простой итерации является метод Зейделя:

Как правило скорость сходимости у метода Зейделя выше, чем в методе простых итераций.
Дана система нелинейных уравнений

(10.5)
Или

В основе метода Ньютона лежит идея линеаризации всех нелинейных уравнений системы (10.5). Разложим каждое уравнение системы (10.5) в ряд Тейлора:
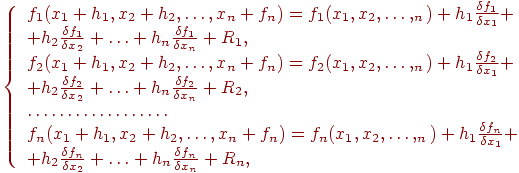
(10.6)
где
hj - приращение по каждой xj; Ri - остаточные нелинейные члены второго и более высоких порядков каждого ряда Тейлора.
Если приращения hj таковы, что переменные xj принимают значения близкие к корню, то будем считать, что левые части уравнений системы (10.6) обращаются в нули. Тогда отбросив Ri сведем задачу решения системы нелинейных уравнений (10.5) к решению системы линейных уравнений, в которой неизвестными являются hj, 
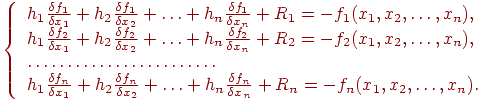
(10.7)
Система (10.7) – система линейных уравнений с неизвестными hj, 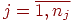 . Запишем (10.7) в матричной форме
. Запишем (10.7) в матричной форме

где

(10.8)

(10.9)
Матрица А, составленая из частных производных ; называется матрицей Якоби, ее определитель- Якобианом.
; называется матрицей Якоби, ее определитель- Якобианом.
На первом этапе реализации метода Ньютона необходимо построить систему (10.3).
На втором этапе, начиная с начальной точки , необходимо решать систему (10.3) на каждом шаге итерационного процесса поиска. Найденные значения приращений hj используются как поправки к решению, полученному на предыдущем шаге поиска, т.е.
, необходимо решать систему (10.3) на каждом шаге итерационного процесса поиска. Найденные значения приращений hj используются как поправки к решению, полученному на предыдущем шаге поиска, т.е.

(10.10)
или

Итерационный процесс прекращается, как только выполнится условие
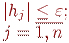
(10.11)
по всем приращениям одновременно. Метод Ньютона имеет преимущества по сравнению с другими методами. Но для метода Ньютона так же существует проблема сходимости, с увеличением числа неизвестных область сходимости уменьшается, а в случае больших систем, сходимость обеспечивается,если начальная точка близка к искомому решению.
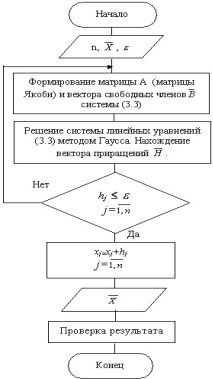
Блок-схема алгоритма метода Ньютона
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 678; Нарушение авторских прав?; Мы поможем в написании вашей работы!