Процедуры

Begin

Else

Begin

Begin

End.

Begin

Begin

Factorial(1)

Factorial(2)

Factorial(3)

Begin

If (n=0)

Then Factorial:= 1 выход из рекурсии

Else Factorial:= n * Factorial(n – 1); рекурсия

End;

При n = 5 эта функция будет работать следующим образом:

Factorial:= 5 * Factorial(4)

5 * 4 * 3 * 2 * 1 = 120

В данном случае реализована так называемая нисходящая рекурсия: вызов Factorial(5) означает, что функция Factorial вызывает себя раз за разом: Factorial(4), Factorial(3), … до тех пор, пока не будет достигнута терминальная ситуация – ситуация окончания рекурсии. При каждом вызове текущие вычисления откладываются, локальные переменные и адрес возврата остаются в стеке. Терминальная ситуация Factorial:= 1 достигается при n = 0. При этом рекурсивный спуск заканчивается, начинается рекурсивный возврат изо всех вызванных в данный момент копий функции: начинает строиться ответ n*Fact(n-1). Сохраненные локальные параметры выбираются из стека в обратной последовательности, а получаемые промежуточные результаты: 1*1, 2*1, 3*2*1, 4*3*2*1, 5*4*3*2*1 – передаются вызывающим функциям.

Рекурсивная функция, вычисляющая n- й член ряда Фибоначчи, может иметь вид:

Function Fibo(n: Word): Word;

If (n=1) Or (n=2)

Then Fibo:= 1 выход из рекурсии

Else Fibo:= Fibo(n-2) + Fibo(n-1); рекурсия

End;

Мы рассмотрели непосредственную рекурсию – функция вызывает саму себя. Помимо непосредственной, возможна косвенная рекурсия – функция Func_1 вызывает функцию Func_2, а функция Func_2, в свою очередь – функцию Func_1. Но как описать две функции, вызывающие одна другую? Ведь по правилам Паскаля подпрограмма обязательно должна быть объявлена до своего использования. В этом случае используется опережающее описание с помощью директивы Forward. При объявлении подпрограммы указывается только ее заголовок со списком формальных параметров и директивой Forward, а тело создается далее без повторного описания этих параметров:

Program Primer;

Uses CRT;

Var i: Integer; описание переменных головной программы

Function Func_1(x: Integer): Integer; Forward; опережающее объявление функции Func_1

Function Func_2(y: Integer): Integer; описание функции

Var k: Integer; Func_2

………

k:= Func_1(y); обращение к функции Func_1

………

End;

Function Func_1; описание функции

Var n: Integer; Func_1 без списка формальных

Begin параметров

……….

n:= Func_2(x); обращение к функции Func_2

……….

End;

Begin основная программа

……..

i:= Func_1(i); обращение к функции Func_1

…….. в основной программе

Примеры:

1. Составить функцию, рекурсивно определяющую значение биномиального коэффициента 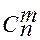при 0<m<n по формулам:

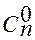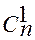= = 1, = +

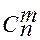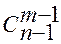
Function Binom(m, n: Word): Word;

If (m=0) Or (m=n)

Then Binom:= 1 выход из рекурсии

Else Binom:= Binom(m, n-1) + Binom(m-1, n-1) рекурсия

End;

2. Составить функцию, рекурсивно определяющую максимальный элемент в заданной части целочисленного массива A_n, начиная с k -го и до n -го элемента:

Const n = 100;

Type TArray = Array [1..n] Of Integer;

………………………………………..

Function Max_element(a: TArray; k,n: Word): Integer;

Var temp: Integer;

If (k=n)

Then Max_element:= a[n]

temp:= Max_element(a, k+1, n);

If (a[k] > temp)

Then Max_element:= a[k]

Else Max_element:= temp

End;

End;

Особенности рекурсии:

· использование рекурсивной формы организации алгоритма выглядит изящнее итерационной и дает более компактный текст программы,

· недостатки рекурсии состоят в следующем:

1. если глубина рекурсии велика, то программа будет требовать во время исполнения много памяти, что может привести к переполнению стека,

2. рекурсивные алгоритмы, как правило, выполняются более медленно,

· при рекурсивном программировании велика вероятность ошибок, вынуждающих программиста к перезагрузке компьютера.

Таким образом, если у программиста есть возможность выбора между итерацией и рекурсией, то предпочтительным выбором является итерация.

В целях повышения безопасности работы рекомендуется:

· для включения проверки переполнения стека необходимо использовать директиву компилятора {S+},

· для включения проверки диапазона необходимо использовать директиву компилятора {R+},

· в начале каждой рекурсивной процедуры или функции поместить строку
If KeyPressed Then Halt. Она позволяет при зависании программы выйти из нее без перезагрузки компьютера, просто нажав любую клавишу.

С математической точки зрения функция выполняет только одно действие – по значению аргументов – фактических параметров вычисляет единственное значение, присваиваемое имени функции. Еще раз напомню, что в функции не рекомендуется использовать параметры-переменные. Если необходимо одновременно вычислить несколько значений, то функцию использовать нельзя.

В этих случаях используют процедуру, которая позволяет одновременно вычислять несколько значений, присваиваемых различным переменным или элементам структур данных.

Как и функция, процедура располагается в вызывающей программе после раздела описания переменных Var и состоит из заголовка, блока описаний и блока операторов.

Заголовок записывается как первая строка процедуры и начинается словом Procedure, за которым следует ее имя. После имени процедуры в скобках перечисляются имена и типы формальных параметров (аргументов процедуры). Заголовок заканчивается точкой с запятой:

Procedure Proc(n,m: Integer; a: Real; Var k: Integer; Var s, d: Real);

Описан заголовок процедуры Proc, зависящей от двух аргументов (входных параметров) целого типа n, m и аргумента a вещественного типа. Выходные (вычисляемые) параметры: переменная k целого типа и переменные s и d вещественного типа.

Допускаются процедуры без списка формальных параметров:

Procedure Zagolovok;

Дата добавления: 2014-01-06