Бинарные деревья

End.

Begin

Begin

End

Repeat

Begin

3 5 7 12

Программа:

Program Sort_spisok;

Uses CRT;

Type TPoint = ^TElement;

TElement = Record

Inf: Integer;

Next: TPoint;

End;

Var head, q, r, v: TPoint;

Procedure Formir_sort_spisok;

New(head); head - указатель на голову списка

head^.Inf:= 0; количество элементов в списке

head^.Next:= Nil; списка еще нет

New(v); формируем первый элемент

Write(‘Первое число: ’);

ReadLn(v^.Inf); вводим его информационную часть

If (v^.Inf=0) если ввели 0,

Then Exit; то выходим из процедуры

head^.Inf:= 1; в списке один элемент

v^.Next:= head^.Next; вставляем его в голову списка

head^.Next:= v; в head^.Next адрес первого элемента списка

New(r); r - поисковая ссылка

New(v); формируем очередной элемент

Write(‘Очередное число: ’);

ReadLn(v^.Inf); вводим его информационную часть

If (v^.Inf=0) если ввели 0,

Then Break; то выходим из цикла ввода

head^.Inf:= head^.Inf + 1; увеличиваем счетчик элементов на 1

r:= head^.Next; поисковик r - на первый элемент списка

q:= head; q – отстает на шаг

While (r <> Nil) Do пока не дошли до конца списка

If (r^.Inf <= v^.Inf) Then если текущий еще меньше

Begin вставляемого,

q:= r; то подтягиваем q к r

r:= r^.Next; и делаем шаг по списку

Else Break; иначе выходим из цикла поиска - место найдено

v^.Next:= q^.Next; ставим новый элемент на место

q^.Next:= v;

Until (v^.Inf = 0);

End;

Procedure Vyvod_spisok; процедура вывода списка

q:= head^.Next; текущую ссылку – на первый элемент

While (q <> Nil) Do пока не конец списка

Write(q^.Inf:5); выводим очередной элемент

q:= q^.Next; ссылку – на следующий элемент

End;

WriteLn;

End;

Begin головная программа

ClrScr;

WriteLn(‘Создание сортированного списка’);

WriteLn;

Formir_sort_spisok; обращение к процедуре создания списка

WriteLn(‘Введено чисел: ’, head^.Inf);

WriteLn(‘Список:’);

Vyvod_spisok; обращение к процедуре вывода списка

ReadLn;

Самым наглядным способом представления информации является ее представление рисунками или графиками. Поэтому при решении многих математических задач используются специальные рисунки (схемы), называемые графами.

Граф представляет собой множество точек – вершин графа, соединенных между собой отрезками – ребрами графа.

Термин граф впервые появился в работах венгерского математика Д.Кенига в 1936 году, хотя ряд задач по теории графов был решен еще Л.Эйлер в XVIII веке.

Примером графа может служить схема линии метрополитена, карта автомобильных или железных дорог. Эти дороги можно рассматривать как ребра, соединяющие города или станции – вершины такого графа.

Вершины графа обычно нумеруются или обозначаются прописными латинскими буквами: A. B, C, … Любой граф можно описать или задать перечислением вершин и ребер. Наиболее удобный способ такого задания – с помощью матрицы смежности, в которой строки и столбцы соответствуют вершинам графа, а значения элементов – длине ребер, соединяющих эти вершины. Если длина ребер не задается, то наличие ребра обозначается единицей, а его отсутствие – нулем.

Например, граф:

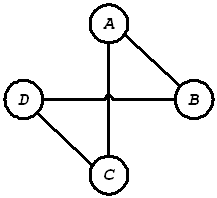
задается матрицей смежности:

A B C D

A

B

C

D

Как видно, это симметричная матрица.

Граф называется ориентированным (орграф), если на каждом его ребре указано направление, то есть о каждой его вершине можно сказать, какие ребра из нее выходят, а какие входят:

Для этого ориентированного графа матрица смежности имеет вид:

Дата добавления: 2014-01-06