Поиск заданного узла в дереве

End.

Begin

Repeat

Begin

Begin

Begin

3 4 4 5 5 7 9 9 14 14 15 16 17 18 20

3 4 4 5 5 7 9 9 14 14 15 16 17 18 20

14 15 4 9 7 18 3 5 16 4 20 17 9 14 5

образует бинарное дерево:

В этом дереве самый левый лист содержит наименьшее число 4, а самый правый – наибольшее 20.

Если сейчас просмотреть это дерево в так называемом симметричном порядке – слева направо: левое поддерево - его корень – правое поддерево, то получим отсортированную последовательность:

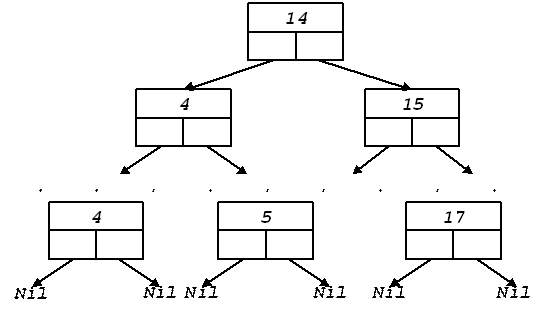Бинарное дерево можно представить связным списком, в котором каждое ссылочное поле каждого элемента (узла) должно содержать значения двух ссылок – на элемент (узел) слева внизу и элемент (узел) справа внизу. Если один из узлов отсутствует, то ссылка на него равна Nil. Самые нижние элементы списка (листья) имеют ссылки со значениями Nil:

Если информационные поля элементов дерева являются данными целого типа, то дерево можно описать, например, следующим образом:

Type TRebro = ^TUzel;

TUzel = Record

Data: Integer; информационное поле

Left, Right: TRebro; ссылочные поля

End;

Var root, q, v: TRebro;

Здесь объектами типа TUzel являются записи, в которых каждое ссылочное поле Left или Right равно либо Nil, либо ссылке на конкретную ячейку памяти компьютера, отведенную для объекта типа TUzel.

Дерево можно представить в виде множества объектов типа TUzel, связанных ссылками. Сами эти объекты соответствуют узлам дерева, а ссылки – его ребрам. Если при этом поле Left (Right) некоторого узла равно Nil, то это значит, что в дереве из этого узла не исходит ребро, направленное влево-вниз (вправо-вниз). Переход от вышестоящего к нижестоящему узлу совершается, как и в связных списках, присваиванием ссылочной переменной значения ее ссылочного поля, левого или правого. Этим способом можно просмотреть все узлы дерева сверху вниз. Включение нового узла в дерево осуществляется, как и включение нового элемента в связный список, изменением значений ссылочных полей соответствующих узлов. Вместе с каждым деревом рассматривается переменная, значением которой является ссылка на корень дерева (в нашем примере это root). Если в дереве нет ни одного узла, то значение этой переменной равно Nil.

Корень дерева можно создать, например, так:

New(root);

Write(‘Первое число: ’);

ReadLn(root^.Data);

root^.Left:= Nil;

root^.Right:= Nil;

После этого можно вводить сортируемую последовательность: очередное введенное число сравнивается с числом, стоящим в корне, и образует левый или правый узел следующего уровня. Ссылку v будем использовать для ввода нового элемента, ссылку q (поисковик) – для поиска места в дереве для нового элемента.

Пример: создать бинарное дерево для сортировки последовательности целых чисел. Ввести несколько чисел (см. выше) – конец ввода – число 0. Вывести введенную последовательность на экран.

Интерфейс:

Первое число: 14

Очередное число: 15

Очередное число: 4

Очередное число: 9

……..

Очередное число: 0

Отсортированная последовательность:

Программа:

Program Bi_Tree;

Uses WinCRT;

Type TRebro = ^TUzel;

TUzel = Record

Data: Integer;

Left, Right: Rebro;

End;

Var root, q, v: TRebro;

Procedure Order(base: TRebro); процедура просмотра дерева

If (base <> Nil) Then

Order(base^.Left);

Write(base^.Data:5);

Order(base^.Right);

End;

End;

ClrScr;

New(root);

Write('Первое число: ');

ReadLn(root^.Data); первое число - в корень дерева

root^.Left:=Nil;

root^.Right:=Nil;

Write('Очередное число: ');

New(v);

ReadLn(v^.Data);

If (v^.Data = 0) если очередное число - ноль,

Then Break; то выходим из цикла ввода

v^.Left:=Nil;

v^.Right:=Nil;

q:=Root; поисковик - в корень дерева

While (q <> Nil) Do пока не добрались до листа:

If (v^.Data < q^.Data) если введенное число меньше числа в очередном узле

Then If (q^.Left <> Nil) и левая ссылка узла не пуста,

Then q:=q^.Left то делаем шаг влево,

Else иначе

Begin если левая ссылка узла пуста,

q^.Left:=v; то подвешиваем туда очередное число

Break; и выходим из цикла поиска

End;

If (v^.Data >= q^.Data) если введенное число больше или равно числу в очередном узле

Then If (q^.Right <> Nil) и правая ссылка узла не пуста,

Then q:=q^.Right то делаем шаг вправо,

Else иначе

Begin если правая ссылка узла пуста,

q^.Right:=v; то подвешиваем туда очередное число

Break; и выходим из цикла поиска

End;

End; {While}

Until (False);

WriteLn;

Writeln('Отсортированная последовательность: ');

Order(root);

WriteLn;

ReadLn;

Задача поиска заданного узла в сформированном дереве сводится к сравнению искомого числа с информационными частями очередных узлов дерева. Добавим в описание переменных предыдущей программы три переменные:

Var poisk: Integer; искомое число

flag: 0..1; флаг поиска; flag=1 – число найдено

n: Word; количество найденных одинаковых чисел

Искомые числа вводить циклом до ввода 0 – конец поиска:

Что искать: 20

Дата добавления: 2014-01-06