
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Закон де Моргана
|
|
|
|
Закон силлогизма
Закон перестановки посылок
Этот закон выражается тавтологией:
A=>(B=>C) ≡ B=>(A=>C)
если из первого высказывания следует, что из второго высказывания следует третье, то из второго высказывания следует, что из первого высказывания следует третье.
Пример: высказывание А=” Сейчас декабрь ”,
высказывание В=” Сегодня 31 число”,
высказывание С=” Завтра Новый Год”,
высказывание A=>(B=>C) =”Если сейчас декабрь, то если сегодня 31 число, то завтра Новый Год”,
высказывание B=>(A=>C) = Если сегодня 31 число, то если сейчас декабрь, то завтра Новый Год”.
Этот закон выражается тавтологией:
(A=>B)& (B=>C) ≡ (A=>C)
если из первого высказывания следует второе, а из второго третье, то из первого высказывания следует третье.
Пример: высказывание А=”Он сдает все работы в срок ”,
высказывание В=”Он получает зачет”,
высказывание С=” Он едет на каникулы”,
высказывание (A=>B)& (B=>C) =”Если он сдает все работы в срок, то он получает зачет, И если он получает зачет, то он едет на каникулы”,
эквивалентно высказыванию (A=>C) =” Если он сдает все работы в срок, то он едет на каникулы”.
Этот закон широко используется при минимизации переключательных функций и выражается формулами:
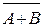 ≡
≡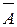 &
&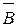
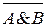 ≡
≡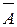 +
+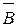
отрицание любого сложного высказывания эквивалентно сложному высказыванию, в котором исходные знаки дизъюнкции заменены знаками конъюнкции, знаки конъюнкции – знаками дизъюнкции, и все составляющие его аргументы – их отрицаниями.
Пример 1: высказывание А – любое,
высказывание В=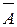 .
.
Тогда 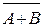 =
= 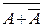 =
= 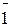 = 0, (под знаком отрицания – закон исключенного третьего)
= 0, (под знаком отрицания – закон исключенного третьего)
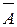 &
&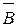 =
=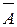 &
&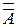 =
= 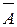 &A = 0.
&A = 0.
Пример 2: высказывание А=”Число заканчивается на 0”,
высказывание В=”Число заканчивается на 5”.
Тогда высказывание A + B =”Число заканчивается на 0 ИЛИ число заканчивается на 5”.
Это признак делимости числа на 5.
Тогда признак неделимости числа на 5 формулируется так 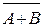 =
=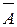 &
&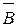 =”Число НЕ заканчивается на 0 И число НЕ заканчивается на 5”.
=”Число НЕ заканчивается на 0 И число НЕ заканчивается на 5”.
Кроме законов, выраженных тавтологиями, в алгебре логики рассматриваются законы (теоремы), позволяющие упростить или преобразовать сложные логические выражения.
К таким законам относятся следующие:
- коммутативный (переместительный) закон:
A + B ≡ B + A
A & B ≡ B & A
- сочетательный закон:
A + (B + C) ≡ (A + B) + C
A & (B & C) ≡ (A & B) & C
- распределительный закон:
A & (B + C) ≡ A & B + A & C
A + B & C ≡ (A + B) & (A + C)
- закон поглощения:
A + A&B = A&(1 + B) = A
A&(A + B) = A&A + A&B = A + A&B = A&(1 + B) = A
- закон склеивания:
A&B + A&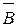 = A&(B +
= A&(B + 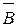 ) = A&1 = A
) = A&1 = A
Кроме этих законов, в алгебре логики рассматриваются следующие соотношения:
A + 0 = A
A + 1 = 1
A & 0 = 0
A & 1 = A
A + A = A
A & A = A
Любую формулу алгебры логики можно представить таблицей истинности, перебрав все значения ее аргументов:
F = A&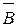 + A&B
+ A&B
| A | B | F |
Любую таблицу истинности можно представить формулой алгебры логики:
| A | B | F |
Оставляем в таблице только те строки, в которых значение функции истинно:
| A | B | F |
Составляем сумму произведений аргументов, причем если значение аргумента ложно, то записываем его с отрицанием:
F = 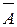 &
&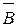 +A&
+A&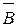
Далее можно упростить эту формулу:
F = 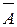 &
&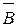 +A&
+A&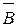 =
= 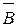 &(
&(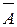 + A) =
+ A) = 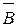 & 1 =
& 1 = 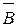
Приложение 2
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 4505; Нарушение авторских прав?; Мы поможем в написании вашей работы!