КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Относительная частота события
|
|
|
|
Классическое определение вероятности
Вероятность – одно из основных понятий теории вероятностей. Существует несколько определений этого понятия. Приведём определение, которое называется классическим.
Рассмотрим пример. Пусть в урне содержится 6 одинаковых шаров, причем 2 шара - красные, 3 – синие и 1 – белый. Необходимо дать количественную оценку возможности того, что взятый на удачу шар цветной. Очевидно, что возможность вынуть наудачу из урны цветной шар больше, чем возможность извлечь белый шар. Эту возможность можно охарактеризовать числом. Это число и называют вероятностью события. Таким образом, вероятность есть число, характеризующее степень возможности появления события.
Рассмотрим событие А – извлечение цветного шара. Каждый из возможных результатов испытаний назовем элементарным исходом. Те элементарные исходы, в которых интересующее нас событие наступает, назовем благоприятствующими этому событию.
Определение: Вероятностью события А называется отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.
Итак, вероятность события А вычисляется по формуле: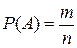 , где
, где 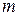 - число благоприятствующих исходов событию А;
- число благоприятствующих исходов событию А; 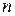 - число всех возможных элементарных исходов.
- число всех возможных элементарных исходов.
Свойства классического определения вероятности:
1. если событие А – достоверное, то 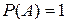 ;
;
2. если событие А – невозможное, то 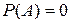 ;
;
3. если событие А – случайное, то 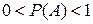 .
.
Пример 1. Человек хотел позвонить по телефону, но забыл одну цифру в номере и набрал её наудачу. Какова вероятность, что цифра набрана верно?
Решение: т.к. в десятичной системе счисления 10 цифр (0..9), а набрана одна цифра то:
m=1 – число благоприятных исходов;
n=10 – общее число исходов;
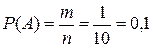 – вероятность возникновения необходимого нам события, в данном случае, это вероятность того, что набрана правильная цифра.
– вероятность возникновения необходимого нам события, в данном случае, это вероятность того, что набрана правильная цифра.
Пример 2. В коробке находится 10 шаров. 3 из них красные, 2 – зеленые, остальные белые. Найти вероятность того, что вынутый наудачу шар будет красным, зеленым или белым.
Решение: Появление красного, зеленого и белого шаров составляют полную группу событий. Обозначим появление красного шара – событие А, появление зеленого – событие В, появление белого – событие С.
Тогда, в соответствием с записанными выше формулами получаем:
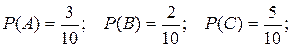
Пример 3. В партии из 10 деталей 7 стандартных. Найти вероятность того, что среди шести взятых на удачу деталей, 4 стандартных.
Решение: Составим схему (см. рис. 1)
7станд 3нест.
4станд и 2нест.
|
Рис 1
Обозначим через А событие – из 6 деталей 4 стандартных.
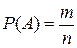
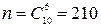
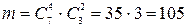
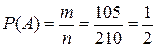
Пример 4. На каждой из 6 одинаковых карточек напечатана одна из букв: а, т, м, р, с, о. Найдите вероятность того, что на 4, вынутых по одной и расположенных в ряд карточках можно прочесть слово «трос».
Решение: Событие А - получение слова «трос»
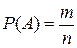
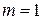
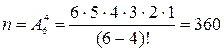
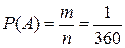
Относительная частота наряду с вероятностью принадлежит к основным понятиям теории вероятностей.
Относительной частотой события называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний. Таким образом, относительная частота события А вычисляется по формуле: 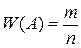 , где
, где 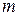 - число появлений события А;
- число появлений события А; 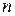 - общее число испытаний.
- общее число испытаний.
Сопоставляя определения вероятности и относительной частоты, делаем вывод: вероятность вычисляют до опыта, а относительную частоту – после опыта.
Длительные наблюдения показали, что если в одинаковых условиях проводят опыты, в каждом из которых число испытаний достаточно велико, то относительная частота обнаруживает свойство устойчивости. Это свойство состоит в том, что в различных опытах относительная частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного числа. Оказалось, что это число есть вероятность появления события.
Таким образом, если опытным путём установлена относительная частота, то полученное число можно принять за приближённое значение вероятности.
Пример. При переборе партии деталей из 80 штук, обнаружено 3 нестандартных детали. Какова частота появления нестандартных деталей в партии?
Решение:
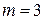
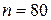
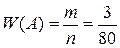 .
.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 6819; Нарушение авторских прав?; Мы поможем в написании вашей работы!