Функция распределения случайной величины

Во всех рассмотренных выше случаях случайная величина определялась путем задания значений самой величины и вероятностей этих значений.

Однако такой метод применим далеко не всегда. Например, в случае непрерывной случайной величины, ее значения могут заполнять некоторый произвольный интервал. Очевидно, что в этом случае задать все значения случайной величины просто нереально. Даже в случае, когда это сделать можно, зачастую задача решается чрезвычайно сложно. Поэтому встает задача по возможности отказаться от индивидуального подхода к каждой задаче и найти по возможности наиболее общий способ задания любых типов случайных величин.

Пусть х – действительное число. Вероятность события, состоящего в том, что Х примет значение, меньшее х, т.е. Х< x, обозначим через F(x).

Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х: .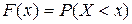

Геометрически это равенство можно истолковать так: F(x) есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.

Функцию распределения также называют интегральной функцией распределения или интегральным законом распределения.

Функция распределения существует как для непрерывных, так и для дискретных случайных величин. Она полностью характеризует случайную величину и является одной из форм закона распределения.

Свойства функции распределения:

1) значения функции распределения принадлежат отрезку [0, 1].

.

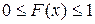2) F(x) – неубывающая функция.

при .

3) Вероятность того, что случайная величина примет значение, заключенное в интервале (a, b), равна приращению функции распределения на этом интервале.

.

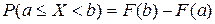4) На минус бесконечности функция распределения равна нулю, на плюс бесконечности функция распределения равна единице.

5) Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю.

Таким образом, не имеет смысла говорить о каком – либо конкретном значении случайной величины. Интерес представляет только вероятность попадания случайной величины в какой – либо интервал, что соответствует большинству практических задач.

Пример 1. Испытывается устройство, состоящее из четырех независимо работающих приборов. Вероятности отказа каждого из приборов равны соответственно р₁=0,3; p₂=0,4; p₃=0,5; p₄=0,6. Построить интегральную функцию распределения.

Решение: Принимая за случайную величину число отказавших приборов, видим что эта случайная величина может принимать значения 0, 1, 2, 3, 4.

Для составления закона распределения этой случайной величины необходимо определить соответствующие вероятности. Примем .

1) Не отказал ни один прибор.

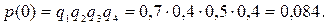
2) Отказал один из приборов.

.

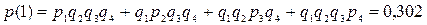3) Отказали два прибора.

4) Отказали три прибора.

5) Отказали все приборы.

Получаем закон распределения:

x
p	0,084	0,302	0,38	0,198	0,036

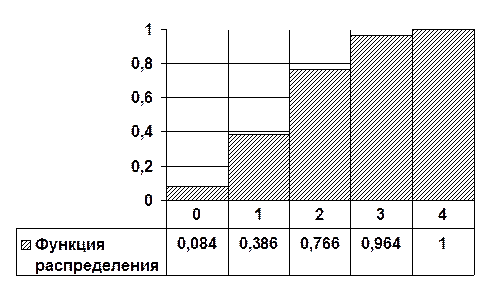Функция распределения будет иметь вид (см. рис. 5):

Рис. 5.

Пример 2: Случайная величина задана функцией распределения

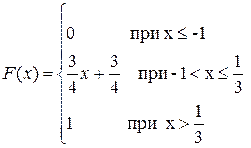
Найти вероятность того, что в результате испытания величина Х примет значение, заключённое в интервале .

Решение:Вероятность того, что случайная величина примет значение, заключенное в интервале (a, b), равна приращению функции распределения на этом интервале . Положив , , получим:

.

Дата добавления: 2014-01-06