
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Разыгрывание полной группы событий
|
|
|
|
Разыгрывание полной группы n (n>2) несовместных событий 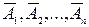 , вероятности которых
, вероятности которых  известны, можно свести к разыгрыванию дискретной случайной величины X со следующим законом распределения (для определенности примем
известны, можно свести к разыгрыванию дискретной случайной величины X со следующим законом распределения (для определенности примем  ,
, 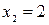 , …,
, …, 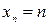 ):
):
| Х | 1 | 2 | … | n |
| p | p1 | p2 | … | pn |
Действительно, достаточно считать, что если в испытании величина X приняла значение  (
(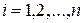 ), то наступило событие
), то наступило событие 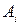 Справедливость этого утверждения следует из того, что число n возможных значений X равно числу событий полной группы и вероятности возможных значений
Справедливость этого утверждения следует из того, что число n возможных значений X равно числу событий полной группы и вероятности возможных значений 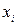 и соответствующих им событий
и соответствующих им событий 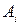 одинаковы:
одинаковы: 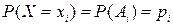 . Таким образом, появление в испытании события А равносильно событию, состоящему в том, что дискретная случайная величина X приняла возможное значение
. Таким образом, появление в испытании события А равносильно событию, состоящему в том, что дискретная случайная величина X приняла возможное значение 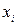 .
.
Правило. Для того чтобы разыграть испытания, в каждом из которых наступает одно из событий 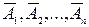 полной группы, вероятности которых
полной группы, вероятности которых  , известны, достаточно разыграть дискретную случайную величину X со следующим законом распределения:
, известны, достаточно разыграть дискретную случайную величину X со следующим законом распределения:
| Х | 1 | 2 | … | n |
| p | p1 | p2 | … | pn |
Если в испытании величина X приняла возможное значение  , то наступило событие
, то наступило событие 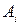 .
.
Пример 1. Заданы вероятности четырех событий, образующих полную группу: 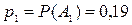 ,
, 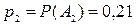 ,
, 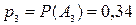 ,
, 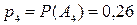 . Разыграть 5 испытаний, в каждом из которых появляется одно из четырех заданных событий.
. Разыграть 5 испытаний, в каждом из которых появляется одно из четырех заданных событий.
Решение: В соответствии с правилом, приведенным в настоящем параграфе, надо разыграть дискретную случайную величину X, закон распределения которой
X 1 2 3 4
р 0,19 0,21 0,34 0,26
По правилу разобьем интервал (0,1) на четыре частичных интервала: 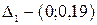 ,
, 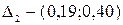 ,
,  ,
, 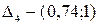 . Выберем из таблицы приложения 5 пять случайных чисел, например: 0,66; 0,31; 0,85; 0,63; 0,73. Так как случайное число
. Выберем из таблицы приложения 5 пять случайных чисел, например: 0,66; 0,31; 0,85; 0,63; 0,73. Так как случайное число  принадлежит интервалу
принадлежит интервалу 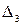 , то Х=3, следовательно, наступило событие
, то Х=3, следовательно, наступило событие  . Аналогично найдем остальные события.
. Аналогично найдем остальные события.
Итак, искомая последовательность событий такова:
 ,
, 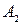 ,
,  ,
,  ,
,  .
.
Пример 2. События А и В независимы и совместны. Разыграть 6 испытаний, в каждом из которых вероятность появления события А равна 0,6, а вероятность появления события В равна 0,2.
Решение: Возможны 4 исхода испытания:
 , причем в силу независимости событий
, причем в силу независимости событий 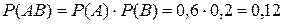 ;
;
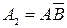 , причем
, причем 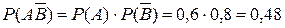 ;
;
 , причем
, причем  ;
;
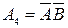 , причем
, причем  .
.
Таким образом, задача сведена к разыгрыванию полной группы четырех событий: 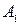 с вероятностью
с вероятностью 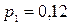 ,
, 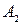 с вероятностью
с вероятностью 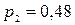 ,
,  с вероятностью
с вероятностью 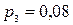 и
и  с вероятностью
с вероятностью 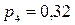 .
.
В свою очередь, в соответствии с правилом настоящего параграфа эта задача сводится к разыгрыванию дискретной случайной величины X, закон распределения которой
| Х | 1 | 2 | 3 | 4 |
| p | 0,12 | 0,48 | 0,08 | 0,32 |
Используем правило. Выберем 6 случайных чисел, например: 0,45; 0,65; 0,06; 0,59; 0,33; 0,70. Построим частичные интервалы:  ,
, 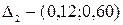 ,
, 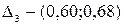 ,
, 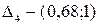 . Случайное число
. Случайное число  принадлежит интервалу
принадлежит интервалу  , поэтому наступило событие
, поэтому наступило событие 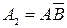 . Аналогично найдем исходы остальных испытаний.
. Аналогично найдем исходы остальных испытаний.
Итак, искомая последовательность исходов разыгранных испытаний такова: 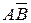 ,
, 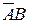 ,
,  ,
, 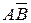 ,
, 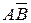 ,
,  .
.
Пример 3. События А и В зависимы и совместны. Разыграть 4 испытания, в каждом из которых заданы вероятности Р(А)=0,8, Р(В)=0,6, Р(АВ)=0,5.
Решение: Возможны 4 исхода испытания:
 , причем, по условию,
, причем, по условию, 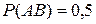 ;
;
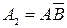 , причем
, причем 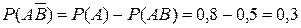 ;
;
 , причем
, причем 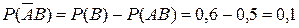 ;
;
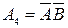 , причем
, причем 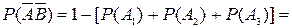
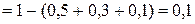 .
.
Таким образом, задача сведена к разыгрыванию полной группы четырех событий: 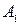 с вероятностью
с вероятностью 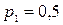 ,
, 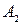 с вероятностью
с вероятностью 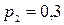 ,
,  с вероятностью
с вероятностью  и
и  с вероятностью
с вероятностью  .
.
Рекомендуем закончить решение самостоятельно, считая для определенности, что выбраны случайные числа: 0,65; 0,06; 0,59; 0,33.
Для контроля приводим ответ: 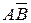 ,
,  ,
, 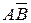 ,
,  .
.
Пояснение. Так как  , то
, то 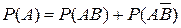 .
.
Отсюда 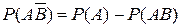 .
.
Аналогично получим, что 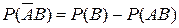 .
.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 3118; Нарушение авторских прав?; Мы поможем в написании вашей работы!