Аналоговые и цифровые сигналы

Пусть х(t) – аналоговый сигнал, а соответствующий ему цифровой сигнал (полученный в результате аналого-цифрового преобразования сигнала х (t) есть х(пТ), где Т – тактовый период, п – номер отсчета аналогового сигнала при его преобразовании в цифровую форму. пТ – тактовые моменты (моменты отсчета аналогового сигнала). При этом будем полагать, что аналоговый сигнал имеет ограниченный спектр и тактовый период удовлетворяет условию T<=1/(2Fmax).

В дальнейшем будем считать, что при t < 0 х(t) = 0 и, следова­тельно, отличные от нуля значения x (пТ) могут иметь место лишь при пТ >= 0 и п представляет собой последовательность (0, 1, 2,...) чисел натурального ряда.

Известно, что операция получения спектральной функции Х (jw) аналогового сигнала х (t) и обратная операция получения сигнала x (t) по известной его спектральной функции Х (jw) производится с помощью пары преобразований Фурье:

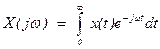(1.1)

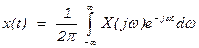(1.2)

Для цифрового сигнала спектральная функция последовательности x[пТ] обозначается Х(е^jωt), а преобразования Фурье определяются следующими выражениями:

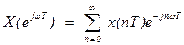(1.3)

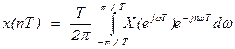(1.4)

Преобразование Фурье, независимо от того, проводится ли оно над аналоговым или дискретным сигналом, и независимо от того, явля­ется оно прямым или обратным, характеризуется следующим свойст­вом: преобразование Фурье, выполняемое над периодической функцией, приводит к дискретной функции, и, наоборот, преобразование Фурье дискретной функции является периодической функцией. Из этого сле­дует, что в случае, если аналоговая функция x (t) является дискретной, то ее спектральная функция является периодической. Если спектр Х(jw) аналогового сигнала х(t) представляется функцией, изображен­ной на рис. 4 а), то после преобразования в цифровую форму сигнал будет описываться дискретной функцией х(пТ) и его спектральная функция будет периодической, как показано на рис. 4 б). Как видно из рис. 4 в пределах интервала -p/T<=w<=p/T модуль спектраль­ной функции аналогового и цифрового сигналов подобны. При ограни­ченном спектре аналогового сигнала спектр цифрового сигнала оказы­вается неограниченным и имеет периодическую структуру с периодом 2pТ. Отсюда следует прием, используемый для получения аналогового сигнала х(t) из цифрового сигнала х(пТ): достаточно цифровую после­довательность преобразовать в последовательность импульсов, име­ющих малую длительность, и амплитуды, равные х(пТ), а затем из спектра такого дискретного сигнала с помощью фильтра нижних частот выделить ту ее часть в интервале 0<=w<=p/Т, которая совпадает со спектром аналогового сигнала. При этом на выходе фильтра образует­ся аналоговый сигнал х(t), соответствующий цифровому сигналу х(пТ).

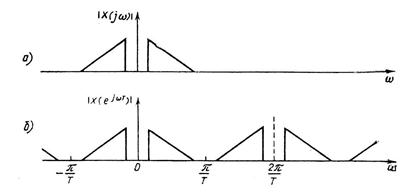
Рис. 4. Спектральные функции: а) непрерывного сигнала; б) дискретного сигнала.

Предположим, что берутся отсчеты непрерывного действи­тельнозначного сигнала x(t) с ограниченным спектром, верхняя частота которого равна F₀ герц, так что НВПФ сигнала x(t) равно нулю при | f|>F₀. НВПФ действительного сигнала x(t) — это всегда симметричная функция с полной шириной спектра, равной 2F₀, Гц; см. рис. 5, а. Отсчеты сигнала x(t) могут быть получены посредством умножения этого сигнала на функцию отсчетов:

x_s(t)=x(t)*TS=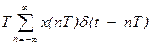 (1.5)

Напомним читателю, что приведенное в (1.5) произведение x(t) с последовательностью импульсных функций должно рас­сматриваться подобно выражению (2.4). В соответствии с теоре­мой свертки в частотной области, НВПФ сигнала х(t) – это просто свертка спектра сигнала x(t) и преобразования Фурье функции отсчетов по времени (TS):

X_s(f)=X(f)*F{TS}= 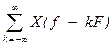(1.6)

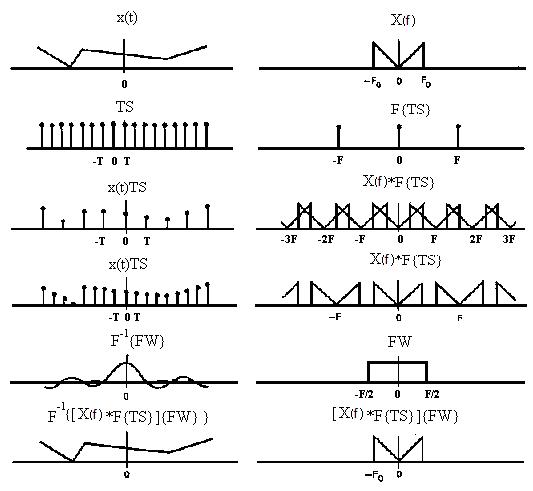
Рис. 5. Иллюстрация теоремы отсчетов во временной области для действи­тельного сигнала с ограниченным спектром: а — исходная функция времени с ограниченным спектром и ее преобразование Фурье; б— функция отсчетов по вре­мени и ее преобразование Фурье; в —временные отсчеты исходной функции и ее преобразование Фурье; в — временные отсчеты исходной функции и ее перио­дическое продолженное преобразование Фурье для случая F₀>1/2T; г— временные отсчеты исходной функции и ее периодически продолженное преобра­зование Фурье для случая F₀<1/2T; д— частотное окно (идеальный фильтр нижних частот) и его преобразование Фурье (функция sinc); e— исходная функция времени, восстановленная посредством операции свертки с функци­ей sinc.

Свертка X(f) с преобразованием Фурье функции отсчетов F{TS}=Ш_l/T(f) просто периодически продолжает X(f) с час­тотным интервалом 1/Т Гц, соответствующим частотному ин­тервалу между импульсными функциями. Поэтому Xs(f) пред­ставляет собой периодически продолженный спектр X(f). Имен­но по этой причине функцию Ш(f) часто называют функцией периодического продолжения. В общем случае отсчеты в одной области (например, временной) приводят к периодическому продолжению в области преобразования (например, частотной). Если частота отсчетов выбрана достаточно низкой, так что F<2F₀, то периодически продолженные спектры будут пе­рекрываться с соседними, как показано на рис. 5, в. Это пе­рекрытие – одна из форм искажения и носит название эффекта наложения в частотной области. Если частота отсчетов повы­шается так, что F>=2F₀, то перекрытие спектров будет отсут­ствовать, что показано на рис. 5, г. Частота отсчетов F_N =2Р₀ получила название частоты отсчетов Найквиста, или частоты сворачивания.

Для того чтобы восстановить исходный временной сигнал по его отсчетам, т.е. осуществить интерполяцию некоторого континуума значений между этими отсчетами, можно пропус­тить дискретизованные данные через идеальный фильтр нижних частот (ФНЧ), обладающий прямоугольной частотной характе­ристикой, показанной на рис. 5, д. В результате (см. рис. 5 ,е):

X(f) =X_s(f) • FW = [X (f) *F{TS}]FW (1.7)

восстанавливается исходное НВПФ. Используя теоремы о сверт­ке во временной и частотной областях, получаем:

х (t) = х_s(t) *F^-1 {FW} = [x (t) • TS] * F^-1 {FW} = 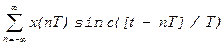(2.37)

Выражение (2.37) представляет собой математическую запись теоремы отсчетов во временной области, которая утверждает, что с помощью интерполяционной формулы (2.37) действитель­ный сигнал с ограниченным спектром может быть точно вос­становлен по бесконечному числу известных временных отсче­тов, взятых с частотой F>=2F₀. Аналогичный подход может быть использован и в случае комплексных сигналов с ограни­ченным спектром с шириной спектра, равной 2F₀ герц.

Дуальной к теореме (2.37) является теорема отсчетов в частотной области. Теперь вместо сигнала с ограниченным спектром рассмотрим действительный сигнал с ограниченной длительностью, т. е. некоторый сигнал x(t), который равен ну­лю при |t|>T₀. Если будем выполнять дискретизацию не во временной, а в частотной области с частотными интервалами F<=1/2T₀ (в противном случае будет возникать наложение во времени), то получим периодическое продолжение неперекры­вающихся сигналов с ограниченной длительностью. Применение идеального прямоугольного временного окна будет восстанавливать ограниченный по длительности исходный сигнал; в час­тотной области это будет соответствовать некоторой операции фильтрации, используемой для восстановления исходного пре­образования. Операции во временной области, характеризую­щие теорему отсчетов в частотной области, описываются выра­жением

x(t)=[x(t)*F^-1{FS}]TW, (1.8)

а операции получения соответствующих преобразований – вы­ражением:

X(f)=[X(f)FS]*F{TW}= 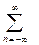Х(n/2T₀)sinc(2Tо[f-n/2T₀)])=

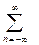= X(nF)sinc([f-nF]/F), (1.9)

описывающим процедуру интерполяции ОД-сигнала, при кото­рой F<=1/2T₀. Таким образом, НВПФ X{f) некоторого сигнала с ограниченной длительностью может быть однозначно восста­новлено по равномерным (эквидистантным) отсчетам спектра такого сигнала, если выбранный интервал отсчетов по частоте удовлетворяет условию F <=1/2Т₀ герц.

.

Дата добавления: 2014-01-06