Типовые законы регулирования. Параметры настройки регуляторов. Классификация объектов автоматического управления

Классификация объектов автоматического управления. Основные свойства объектов автоматического управления мясной и молочной промышленности.

Объекты мясной и молочной промышленности можно отнести к следующим группам со сходными динамическими свойствами:

Одноемкостные объекты те, скорость изменения выходной величины которых при подаче на вход ступенчатого воздействия постоянная или непрерывно уменьшается с течением времени от максимального, соответствующего начальному моменту времени, до нуля. Напомним, что емкость объекта Е характеризует его способность накаливать вещество или энергию. Уравнения динамики для этой группы соответствуют интегрирующему звену для астатических объектов или апериодическому 1-го порядка для статических. Одноемкостные статические объекты обладают способностью самовыравнивания. Моделями 1-го порядка удовлетворительно описываются динамические свойства большого числа технологических объектов управления в мясной, молочной и рыбной промышленности. Напомним, что модель 1-го порядка содержит следующие параметры, которые необходимо найти (рассчитать): коэффициент передачи К, постоянную времени Т. (см.раздел 1.4). Многоемкостные объекты состоят из последовательно соединенных звеньев. Для упрощения математического описания многоемкостные объекты часть представляют в виде последовательно соединенных одноемкостного (статического или астатического) и объекта запаздывания. (рисунок 28). К объектам запаздывания относятся трубопроводы, транспортеры. Состояние объектов с распределенными параметрами невозможно охарактеризовать заданием регулируемых величин только во времени. Состояние этих объектов описывают дифференциальными уравнениями в частных производных, интегральными и интегродифференциальными уравнениями. К объектам с распределенными параметрами относятся пастеризационные установки, термокамеры.

Рис.28. Графики переходных характеристик многоемкостных объектов и их структурные схемы после аппроксимации: а – статического; б – астатического.

Закон регулирования – это математическая зависимость, с помощью которой определяется регулирующее воздействие u(t) по сигналу рассогласования e(t) (рисунок10). По характеру изменения регулирующего воздействия различают линейные и нелинейные, дискретные и непрерывные законы регулирования. В инженерной практике наибольшее применение имеют типовые линейные законы регулировании: пропорциональный (П), интегральный (И), пропорционально-интегральный (ПИ), пропорционально-интегрально-дифференциальный (ПИД). Регуляторы, работающие по этим законам, называют П-(пропорциональный или статический), И- (интегральный или астатический), ПИ- (пропорционально -интегральный или изодромный), ПИД-регуляторами (регулятор с предварением- пропорционально-интегрально-дифференциальный.). Коэффициенты и постоянные времени, входящие в законы, называют параметрами настройки (уставками). Они позволяют обеспечить необходимый характер переходного процесса регулирования для объектов с различными динамическими свойствами. Кроме органов настройки, непосредственно воздействующих на параметры, входящие в закон регулирования, регуляторы имеют органы настройки, косвенно влияющие на режим работы САР, такие, как чувствительность регулятора и др.

Характеристики регуляторов непрерывного действия и переходные процессы регулирования в статическом объекте приведены на рисунке 29.

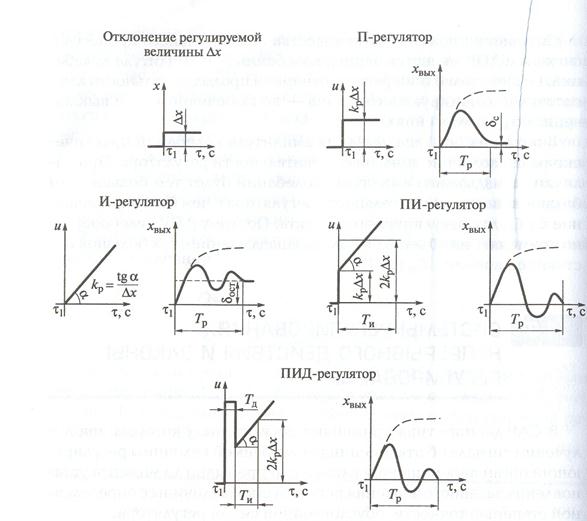
Рис. 29. Характеристики регуляторов непрерывного действия

П-регулятор по динамическим характеристикам является безинерционным звеном, коэффициент передачи которого Кр численно равен перемещению РО при единичном отклонении регулируемой величины от заданного значения, т.е. u(t) = Kp e(t), а передаточная функция W(p) = K_p, где K_p - коэффициент передачи.

Настроечный параметр этого регулятора представляют не в форме K_p, а в виде величины δ, обратно пропорциональной коэффициенту передачи. Эту величину называют степенью неравномерности или диапазоном дросселирования (в пневматических регуляторах) – см. рис.20. Степень неравномерности, выраженная в процентах, характеризует степень отклонения регулируемой величины (в процентах от максимально возможной для данной САР), которая соответствует перемещению РО из одного крайнего положения в другое. Главным достоинством П-регуляторов является простота их реализации и настройки. При наличии возмущающих воздействий регулятор быстро приводит к в равновесное состояние почти любой объект. Положение РО однозначно связано с отклонением регулируемого параметра от заданного значения, что обуславливает статическую ошибку – основной недостаток П-регуляторов.

И-регулятор по динамическим свойствам соответствует интегрального звену. Он перемещает РО пропорционально интегралу от отклонения регулируемой величины u(t) = Ks ∫e(t)dt. Коэффициент передачи Кs равен скорости перемещения РО при отклонении регулируемой величины на единицу ее измерения. Интегральный регулятор перемещает РО до тех пор, пока регулируемая величина не достигнет заданного значения. САР с И-регулятором не имеет статической ошибки и является астатической. Передаточная функция И-регулятора:

W(s) = Ks / (Tи s ), где Ти – постоянная величина интегрирования (постоянная изодрома), равная времени, в течение которого выходной сигнал регулятора достигает значения входного сигнала. И-регуляторы способы устойчиво регулировать лишь объекты, обладающие самовыравниванием. Для них характерна относительно невысокая скорость регулирования, при этом она обратно пропорциональна Ти. И-регуляторы используют, в основном, при построении ПИ- и ПИД-регуляторов.

ПИ-регуляторы (изодромные) сочетают преимущества П- и И-регуляторов и обеспечивают устойчивое регулировании (без статической ошибки) большинства объектов. Математическое выражение закона ПИ-регулирования: u(t) = K_s[e(t) + (1/T_u) ∫ e(t)dt]. В И-регуляторе после скачкообразного изменения сигнала рассогласования регулирующий орган под воздействием пропорциональной составляющей мгновенно переходит в новое положение, определяемое произведением Ке, а затем под воздействием интегральной составляющей перемещается с постоянной скоростью Ке /Ти. С ростом Ти влияние интегральной составляющей на процесс регулирования уменьшается. Передаточная функция ПИ-регулятора имеет вид: W(s) = K_s (1 + 1/T_us). Параметры настойки: коэффициент передачи Кs и постоянная интегрирования Ти.

ПИД-регуляторы по динамическим свойствам воздействуют на объект пропорционально отклонению регулируемой величины, интегралу от этого отклонения и скорости изменения регулируемой величины. Математическое выражение ПИД закона регулирования: u(t) = K_s[e(t) + 1/T_u ∫ e(t)dt + T_n de(t)/dt], где Т_и – постоянная интегрирования, Т_п – время предварения. ПИД-регуляторы интегральные (изодромные) регуляторы с предварением, т.е. они реагируют не только на отклонение регулируемой величины от заданной, но и на тенденцию ее изменения. Структурно ПИД-регулятор можно представить как систему из 3-х параллельно включенных безинерционного, интегрирующего и дифференцирующего звеньев. Передаточная функция ПИД-регулятора:

W(s) = Ks(1 + 1/T_us+ Т_пs).

ПИД-регулятор при скачкообразном изменении регулируемой величины в начальный момент времени оказывает мгновенное бесконечно большое по амплитуде воздействие на объект, затем величина воздействия уменьшается до значения, определяемого пропорциональной частью регулятора. Далее реализуется ПИ функция (рис.21). Наличие дифференцирующей составляющей улучшает эффект регулирования при действии на объект значительных переменных воздействий (нагрузок). Однако настойка ПИД-регулятора, связанная с определением трех параметров (Кs, Ти, Тп) сложна, при неправильной настройке качество регулирования может оказаться хуже, чем при использовании более простых регуляторов.

Параметры настроек рассмотренных регуляторов определяют расчетным путем на основании динамических свойств объекта (статический, астатический) и заданных требований к процессу регулирования – по формулам для приближенного расчета.

В САР прерывистого действия применяются регуляторы дискретного релейного типа. Позиционные регуляторы широко используются при автоматизации технологических процессов. Наиболее простым из них является двухпозиционный регулятор (ДПР), у которого рабочий орган может занимать только два положения — полностью открыт или полностью закрыт, что соответствует максимальному и минимальному регулирующему воздействию. Характеристика ДПР приведена графически на рисунке 30 а, где видно, что отклонение регулируемой величины ∆х от заданного значения x_о на величину большую ε (диапазон наибольших отклонений регулируемой величины от заданного значения, не вызывающих срабатывания регулятора), вызывает срабатывание регулятора и управляющее его воздействие равно Q_mах или Q_min в зависимости от знака отклонения.

Переходный процесс в статической САР с двухпозиционным регулятором (рис.30,6) носит характер незатухающих колебаний; на рис. 30, в приведен график соответствующего положения регулирующего органа.

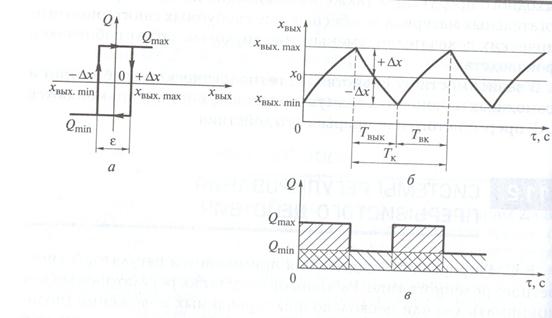
Рис. 30.Автоматическая система регулирования с двухпозиционным регулятором:

a — график регулирующего воздействия; б — переходной процесс регулирования; в — положение рабочего органа

Основными показателями качества колебательного процесса в системе с ДПР являются период колебаний Т_к и амплитуда колебаний Тк. Период колебаний равен суммарной продолжительности двух состояний регулирующего органа — во включенном Т_ВК и выключенном Твык положениях.

В объектах без запаздывания амплитуда колебаний практически равна половине зоны нечувствительности регулятора. При наличии запаздывания амплитуда колебаний будет тем больше, чем больше зона нечувствительности регулятора и чем больше отношение τ₃/ Т_об для регулируемого объекта. Поэтому ДПР целесообразно применять на объектах с малым запаздыванием τ ₃ и большой постоянной времени Т_об. то есть 0< τз/ Tоб < 0,2

Системы со средствами вычислительной техники в контуре управления относятся к дискретным системам, которые функционируют в дискретном временном пространстве и определяются дискретными состояниями (рис.22) В такой системе, в отличие от непрерывной, управляющее устройство оперирует с дискретными числовыми последовательностями, получаемыми путем квантования по времени непрерывной функции (рис.23). Обычно в цифровых системах квантование производится с постоянным интервалом времени (интервалом дискретности Т). Преобразование непрерывного сигнала в числовую последовательность осуществляется в аналого-цифровом преобразователе (АЦП). В вычислительном устройстве (ВУ) определяется текущее значение управляющего воздействия, которое преобразуется затем из числового (дискретного) в непрерывный (аналоговый) сигнал с помощью цифро-аналогового преобразователя (ЦАП). Для управления технологическими процессами часто используют хорошо исследованные линейные законы регулирования, реализуемые в дискретной форме в ВУ. В этом случае определяют параметры настройки, рассмотренные выше, а также рассчитывают интервал дискретности. Управляющее вычислительное устройство (контроллер) одновременно обслуживает несколько контуров управления.

Рис. 31. Структурная схема САР с цифровым вычислительным устройством

Рис. 32. Графики непрерывной функции (аналоговый сигнал- а) и дискретной последовательности (б -).

Дата добавления: 2014-01-06