Формула Бернулли

Теория вероятностей

(для студентов специальности «Информатика»)

Тема 2. ПОВТОРНЫЕ НЕЗАВИСИМЫЕ ИСПЫТАНИЯ

Простейшим классом повторных независимых испытаний является последовательность независимых испытаний с двумя исходами: событие А осуществилось и не осуществилось , причем вероятность этих исходов не меняется от испытания к испытанию. Вероятность наступления события А в каждом испытании обозначим через р, т.е. Р(А) = р. Тогда Р(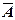) = 1 – р = q. Пусть m – число (частота) наступления события А в n испытаниях. Обозначим через Р_{m, n} – вероятность того, что частота появления события А равна именно m. Эта вероятность может быть посчитана по формуле Бернулли

(1)

Числа Р_m,n также интерпретируется как вероятность иметь ровно m осуществлений события А в n независимых испытаниях с двумя исходами. Вероятность того, что частота m появления события А в n испытаниях примет значение из промежутка [ m ₁, m ₂] (m ₁ £ m £ m ₂) равна

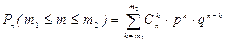(2)

Вероятность того, что событие А хотя бы один раз наступит в n испытаниях вычисляется по формуле

Р _n (m ³ 1) = 1 – Р _0,n = qⁿ

§2. Формула Пуассона.

Нередко приходится рассматривать эксперименты с большим числом испытаний. Нетрудно видеть, что для больших n и m вычисление вероятностей по формуле Бернулли представляется значительные затруднения, становятся очень громоздкими. В этом случае применяются приближенные формулы, позволяющие с достаточной степенью точности найти эти вероятности. Если число испытаний достаточно велико, а р мало и при этом произведение n×p – не больше 10, то вероятность Р_{m, n} можно найти по формуле Пуассона

(3)

Вычисления по формуле (3) существенно упрощаются, если используются специальные таблицы.

Замечание. Вероятность того, что в испытаниях событие наступит: а) менее k раз; б) более k раз; в) не менее k раз; г) не более k раз, – находят соответственно по формулам:

а) Р_{0, n} + Р_{1, n} + … + Р _{k–1, n}.

б ) Р_{k+1, n} + Р _{k+2, n} + … + Р_{n, n}.

в) Р_{k, n} + Р_{k+1, n} + … + Р_{n, n}.

г) Р_{0, n} + Р_{1, n} + … + Р_{k, n}.

Дата добавления: 2014-01-06