Стабилизация управляемых колес

Стабилизацией называют свойство управляемых колес сохранять нейтральное положение, соответствующее прямолинейному движению, и автоматически в него возвращаться /7/.

Управление автомобилем с плохой стабилизацией затруднено, и движение его неустойчиво, автомобиль постоянно отклоняется в стороны, и водитель вынужден поддерживать требуемое направление движения.

Управляемые колеса возвращаются в нейтральное положение под воздействием стабилизирующего момента. Возникновение стабилизирующих моментов связано в основном двумя причинами:

1) взаимодействием эластичных шин с опорной поверхностью;

2) наклоном шкворней поворотных цапф.

11.6.1. Стабилизирующие моменты шины

Рассмотрим взаимодействие шины, катящейся по опорной поверхности с боковым уводом.

При качении с уводом оси Х₁ и Y₁ пятна контакта колеса поворачиваются относительно своего обычного положения (осей X и Y) на некоторый угол d, а само колесо смещается относительно центра пятна (точка О₁) вдоль оси Y на величину d (рис. 70,а).

Рис. 70. Эпюры распределения элементарных боковых реакций и точки приложения результирующих сил

Как показывают исследования, при отсутствии в пятне контакта зон относительного проскальзывания эпюра распределения элементарных боковых реакций имеет вид, близкий к треугольнику (рис. 70,б). При этом наибольшие значения элементарных боковых реакций наблюдается в зоне наибольших боковых деформаций шины (заштрихованная часть пятна контакта на рис. 70,а). При дальнейшем увеличении боковой силы и возрастании угла увода d (рис. 70,в) эпюра элементарных боковых реакций приобретает форму трапеции. Это объясняется тем, что в задней части пятна контакта (зона Dх на рис. 70,а и в) дальнейший рост элементарных реакций прекращается и возникает боковое скольжение.

Из-за несимметричности распределения элементарных боковых реакций точка приложения боковой реакции R_у1 оказывается сдвинутой в заднюю часть пятна контакта на некоторое расстояние e относительно проекции центра колеса на опорную плоскость (точка О) и центра пятна контакта (точка О₁). Вследствие несимметричности эпюр нормальных и касательных реакций точки приложения результирующих сил R_z1 и R_x1 также смещаются относительно точки О соответственно на расстояние a, b и d (рис. 70,а). При этом смещение R_у на расстояние е создает так называемый поперечный стабилизирующий момент шины:

M_су = R_уe = K_увde. (263)

Смещение вектора R_x на расстояние d дает продольный стабилизирующий момент шины:

M_сх = R_xd. (264)

Смещение вектора R_z на расстояние а создает, как указывалось выше, момент сопротивления качению (M_f = R_za).

Алгебраическую сумму моментов M_су и M_сх называют полным стабилизирующим моментом шины:

M_сш = M_су + M_сх = R_уe - R_хd. (265)

Рассмотрим, от чего зависит величина указанных стабилизирующих моментов.

При увеличении d значение поперечного стабилизирующего момента (M_cу) вначале возрастает, а при достижении 6 - 8^о снижается. Такой характер зависимости M_су = f(d) объясняется следующим.

Увеличение d, согласно (250), приводит к возрастанию M_су. При этом плечо е почти не изменяется. Когда угол бокового увода d достигнет значения 3 - 5^o, в зоне Dх пятна контакта (рис. 70,а и в) возникает проскальзывание и эпюра элементарных боковых сил принимает трапециедальный характер (рис. 70,в). Это вызывает приближение линии действия боковой реакции R_у к центру пятна контакта, т.е. уменьшение плеча e.

Рис. 71. Зависимость поперечного стабилизирующего момента шины от угла увода при разных вертикальных нагрузках (G_к1 < G_к2 < G_к3)

Действие стабилизирующих моментов шин управляемых колес проявляется следующим образом. Предположим, что при движении автомобиля управляемые колеса, получив толчок от неровности дорожного полотна, повернулись на некоторый угол q, причем (d = q) шины будут испытывать боковой увод. В результате боковой деформации шин и смещения линий действия продольных и поперечных сил последние образуют моменты, стремящиеся вернуть колеса в исходное положение. При этом поперечные стабилизирующие моменты шин на левом и правом колесе действуют в одном и том же направлении (рис. 72), стремясь вернуть колеса в исходное положение.

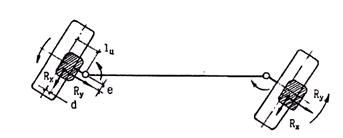
Рис. 72. Образование стабилизирующих моментов при случайном

повороте управляемых колес

В отличие от поперечных реакций, продольные реакции (R_x) образуют моменты относительно осей поворота колес (шкворней), которые действуют в противоположных направлениях, вследствие чего они в значительной мере компенсируют друг друга. Однако момент от продольной реакции на левом колесе равен R_x(l_ц- d), а на правом - R_x(l_ц+ d). Поэтому результирующий момент на колесах равен сумме продольных стабилизирующих моментов шин:

М_cx = R_x(l_ц + d) - R_x(l_ц - d) = 2R_xd. (266)

Заметим, что в рассматриваемой ситуации моменты М_cx не играют стабилизирующей роли, т.к. противодействуют поперечным стабилизирующим моментам шин и стремятся не сократить, а увеличить угол поворота управляемых колес. Величины d и R_x, как правило, малы, поэтому моменты М_cx не могут заметно ухудшить стабилизацию управляемых колес. Однако в тех случаях, когда величина продольных реакций резко возрастает (например при интенсивном торможении), моменты М_cx становятся ощутимыми и оказывают значительное влияние на стабилизацию управляемых колес.

Если управляемые колеса автомобиля одновременно являются и ведущими, то продольные усилия направлены в противоположную сторону, вследствие чего моменты М_cx становятся действительно стабилизирующими, т.к. способствуют возврату колес в исходное положение.

11.6.2. Стабилизирующие моменты за счет наклона и сдвига оси поворота колеса

У современных автомобилей оси поворота управляемых колес имеют продольный и поперечный наклон. При этом у грузовых автомобилей и автобусов, имеющих неразрезную балку переднего моста, положение оси поворота определяется положением шкворня, а у легковых автомобилей, имеющих, как правило, независимую подвеску управляемых колес, - центрами шаровых шарниров. За счет продольного наклона оси поворота (рис. 73,а) плечо действия боковой реакции R_у возрастает от е до е' = е сosb_оп + r_д sinb_оп. Это приводит к соответствующему увеличению поперечного стабилизирующего момента шины:

M_су = R_у(е сosb_оп + r_д sinb_оп)» R_у(е + r_дb_оп), (267)

где b_оп - угол продольного наклона оси поворота колеса (шкворня).

а б

Рис. 73. Стабилизирующий момент при продольном наклоне (а) и сдвиге (б) оси поворота управляемых колес

Величины углов b_оп у разных автомобилей неодинаковы. Чаще всего он назначается в пределах от 0 до 4^о. У некоторых легковых автомобилей из-за особенностей кинематической схемы подвески угол продольного наклона может изменяется в зависимости от величины действующей нагрузки и достигать значений 10 - 12^о. Иногда для уменьшения автоколебаний управляемых колес у легковых автомобилей продольный наклон оси делают отрицательным.

Увеличить плечо действия боковой силы можно не только за счет продольного наклона оси поворота, но и за счет ее смещения вперед относительно оси вращения колеса на некоторую величину De (рис. 73,б). Как и при наклоне оси, возрастание плеча приводит к возрастанию поперечного стабилизирующего момента на величину DM_су = R_у De.

Для стабилизации управляемых колес при очень малых скоростях оси их поворота имеют наклон в поперечной плоскости (рис. 74).

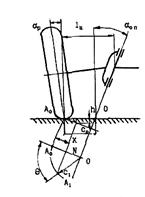
Рис. 74. Возникновение стабилизирующего момента при поперечном

наклоне оси поворота колеса:

a_оп - угол поперечного наклона; a_р - угол развала; l_ц - длина цапфы; с_o - плечо обкатки.

При этом у большинства современных автомобилей углы a_оп назначаются в пределах 4 - 10^о. Наличие наклона осей шкворней приводит к тому, что при повороте управляемых колес на угол q происходит подъем передней части автомобиля на высоту h. Это объясняется тем, что точка А_о при повороте колеса вокруг оси поворота должна перемещаться по дуге А_оА₁ и опустится вниз на величину h относительно опорной поверхности. Та как в действительности этого произойти не может, поворот колеса вызовет подъем передней оси автомобиля на эту величину. При этом передняя часть автомобиля приобретает запас потенциальной энергии, равный dП = G_а1dh (G_а1 - вес автомобиля, приходящийся на передний мост). Работа, совершаемая при повороте управляемого колеса: dA = Мdq. Из равенства dП и dA следует, что величина прикладываемого момента равна:

М = G_а1dh/dq. (268)

Данная величина крутящего момента численно равна (если не учитывать трение в сочленениях рулевого привода) моменту, который препятствует повороту колес, т.е. стабилизирующему моменту.

Установим влияние угла наклона осей поворота колес (a_оп), угла поворота управляемых колес (q) и веса автомобиля, приходящегося на управляемые колеса (G_а1), на величину стабилизирующего момента. Из рис. 74. следует:

h = x sina_оп; (269)

х = А_oО - NO = (с₁ - с₁cosq); (270)

c₁= с_ocosa_оп; (271)

dh/dq = c sinq sina_оп. (272)

Учитывая (269 - 272), величину стабилизирующего момента можно выразить формулой:

М_cz = G_а1с₁sina_опsinq. (273)

Таким образом, при повороте управляемых колес на угол q создается стабилизирующий момент, стремящийся вернуть их в исходное положение. Так как величина стабилизирующего момента прямо пропорциональна весу автомобиля, приходящемуся на переднюю ось, то М_cz называют весовым стабилизирующим моментом.

Дата добавления: 2014-01-06