Некоторые термины и определения, используемые при решении задач оптимизации

ОПТИМИЗАЦИЯ РАЗРАБОТОК

Блочно-иерархический подход при проектировании искусственных систем

Основу мышления проектировщика составляет блочно-иерархический подход. При блочно-иерархическом подходе (частном эвроритме системного подхода, который используется часто в технике и программировании) процесс проектирования и представления о самом объекте расчленяется на уровни. На высшем уровне используется наименее детализированное представление, отражающее самые общие черты и особенности проектируемой системы. На каждом новом последовательном уровне разработки степень подробности рассмотрения возрастает, при этом система рассматривается не в целом, а отдельными блоками.

Методология блочно-иерархического подхода базируется на трех концепциях: разбиения и локальной оптимизации; абстрагирования; повторяемости.

Концепция разбиения позволяет сложную задачу проектирования объекта или системы свести к решению более простых задач с учетом их взаимосвязи. Локальная оптимизация подразумевает улучшение параметров внутри каждой простой задачи. Абстрагируемость заключается в построении моделей, отражающих только значимые в данных условиях свойства объектов. Повторяемость заключается в использовании существующего опыта проектирования.

Блочно-иерархический подход позволяет на каждом уровне решать задачи приемлемой сложности. Разбиение на блоки должно быть таким, чтобы документация на блок любого уровня была обозрима и воспринимаема одним человеком.

Главным недостатком блочно-иерархического подхода является то, что на верхних уровнях имеют дело с неточными моделями объекта и решения принимаются в условиях недостаточной информации. Следовательно, при этом подходе высока вероятность проектных ошибок.

При постановке и решении задач оптимизации используются термины из разных областей научных и технических знаний: математического программирования, математического моделирования, теории управления, квалиметрии. Для устранения терминологической путаницы введены следующие понятия, которые наиболее часто используются специалистами в данной области.

Минимизируемая (целевая) функция Q(Х) представляет собой функцию обобщенного показателя качества. Глобальный экстремум данной функции Q*(X*) обычно соответствует оптимальному решению.

Обобщенный показатель качества - это выражение целевой функции через частные показатели качества.

Показатель (критерий) качества - численная характеристика (оценка) отдельных свойств конструкции.

Пространством показателей называется пространство, координатами точек которого являются оценки по соответствующим критериям.

Если требуется оптимизировать совокупность отдельных показателей, то задача называется задачей векторной оптимизации.

Если оптимальность определяется лишь по одному показателю, то задача называется задачей скалярной оптимизации.

Функция Q(Х) может быть как одномерной, так и многомерной. Соответственно говорят об одномерной и многомерной оптимизации.

Параметры объекта (процесса) могут называться параметрами математической модели, параметрами целевой функции, переменными целевой функции или просто параметрами (переменными). Если параметры могут принимать только заранее установленные дискретные значения (например, резьбы: М2, М3...), то ставится задача дискретной оптимизации. Частным случаем дискретной оптимизации является целочисленная оптимизация, когда параметры могут принимать только целые значения.

Ограничением называется соотношение, задающее область существования целевой функции Q(X). Ограничения могут быть параметрическими и функциональными. Параметрические ограничения задают область изменения конкретных параметров, функциональные ограничения представляют собой равенства или неравенства. Примеры ограничений:

x_i>0 - одностороннее параметрическое ограничение;

a_j≤x_j≤b_j - двустороннее параметрическое ограничение;

G_i(X)=0 - функциональное равенство;

D_j(X)≥0 - функциональное неравенство.

Если все ограничения двусторонние параметрические, то говорят об области, ограниченной в виде гиперпараллелепипеда.

Оптимизация целевой функции без ограничений называется безусловной оптимизацией. В противном случае - условной оптимизацией.

Целеваяфункциявзадачахоптимизацииневсегдазадаетсяявно. Ряд методов оптимизации позволяет находить оптимальные значения X* по значению производной от целевой функции. Методы поиска, в которых для нахождения оптимального значения используются лишь расчет значений целевой функции, называются методами прямого поиска. При этом рассчитанные значения целевой функции и значения их аргументов в необходимых для метода точках называются пробами.

Градиентом целевой функции Q(X) в точке X⁰=(x₁⁰,x₂⁰,...,x_n⁰) называется вектор, составленный из первых частных производных функции в этой точке. Геометрически градиент указывает направление возрастания функции в данной точке X=X⁰. Модуль (величина) градиента характеризует скорость возрастания функции в заданной точке X⁰ и вычисляется по формуле

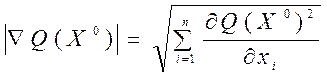
где V - оператор "набла".

Если для любых точек функции Q grad(Q) = const, то функция линейна. Линейная функция одновременно выпуклая и вогнутая. Пример линейной функции:

Q = 2x₁+3x₂-4x₃+2x₄; grad(Q) = 2+3-4+2 = 3 = const.

Дата добавления: 2014-01-06