Напряжения в балке при чистом изгибе

Лекция 8

Поставим перед собой задачу найти закон, по которому распределены напряжения в сечениях изогнутой балки. Рассмотрение начнём с самого простого случая, а именно – чистого изгиба, при котором в поперечных сечениях возникает только один внутренний силовой фактор – изгибающий момент. При этом, как и раньше, будем предполагать изгиб плоским.

В качестве примера возникновения чистого изгиба может служить консольная балка, нагруженная сосредоточенным моментом на конце (рис. 8.1).

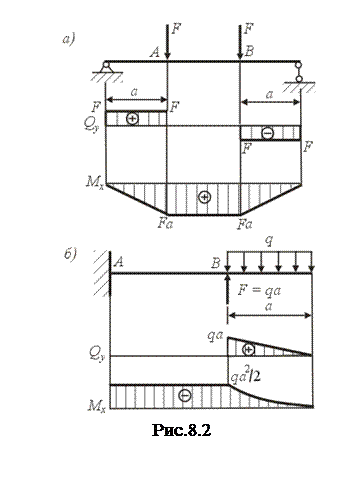Поперечные силы в такой балке отсутствуют, а изгибающий момент постоянен по её длине. Стоит отметить, что, несмотря на некоторую искусственность такого нагружения, чистый изгиб встречается на практике довольно часто. Дело в том, что появление чистого изгиба возможно при нагружении не только моментами, но также сосредоточенными и распределёнными силами. Так, участки АВ балок, изображённых на рис. 8.2, испытывают чистый изгиб.

Как отмечалось в самом начале изучения курса “Сопротивление материалов”, с помощью метода сечений и уравнений статики можно определить главный вектор и главный момент распределённых по сечению внутренних сил. Но для определения закона, по которому распределяются напряжения, одних уравнений равновесия недостаточно – необходимо привлечь условия деформации балки. Здесь на помощь вновь приходят экспериментальные данные. Рассмотрим балку, из легко деформирующегося упругого материала (например, поролона), на боковую поверхность которой нанесена сетка из продольных и поперечных прямых. Если подвергнуть такую балку чистому изгибу, то окажется, что продольные линии изогнутся, а поперечные останутся прямыми, повернувшись на некоторый угол. (рис. 8.3).

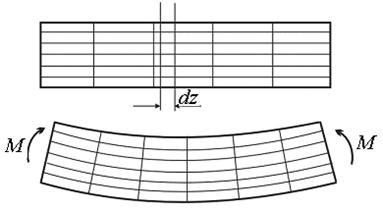
Рис. 8.3

Это обстоятельство, а также некоторые несложные рассуждения приводят к выводу, что при чистом изгибе, как и при осевом растяжении справедлива гипотеза плоских сечений – поперечные сечения, плоские до нагружения, остаются таковыми и после приложения нагрузки. Таким образом, деформацию при чистом изгибе можно рассматривать как результат взаимного поворота плоских поперечных сечений.

Мысленно вырежем из участка балки, находящегося в состоянии чистого изгиба, бесконечно малый элемент длиной dz (рис. 8.4)

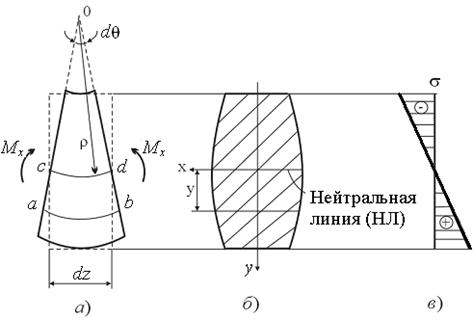
Рис. 8.4

Недеформированное состояние элемента показано пунктиром. После нагружения элемент искривляется. Поперечные сечения, которыми он выделен, поворачиваются в плоскости чертежа на некоторый малый угол d q. При этом верхние волокна элемента укорачиваются, нижние – растягиваются. Зону сжатия от зоны растяжения будет отделять слой волокон, длина которых остаётся прежней – dz. Этот слой волокон, не меняющий при изгибе своей длины, называют нейтральным слоем, он отмечен на рис. 8.4, а отрезком cd. Пересечение нейтрального слоя с плоскостью поперечного сечения образует прямую, которую называют нейтральной линией (см. рис. 8.4, б). Ось Оx, проходящая через нейтральную линию, называется нейтральной осью. По ширине балки все волокна деформируются одинаково.

Обозначим величиной ρ радиус кривизны нейтрального слоя. При этом ни положение нейтрального слоя, ни его кривизна нам пока неизвестны. Длину нейтрального слоя dz можно выразить через радиус кривизны и угол поворота сечений следующим образом:

dz = ρ d q (8.1)

Обозначим длину слоя волокон, лежащих на произвольном расстоянии у от нейтрального слоя, отрезком аb, тогда будем иметь

аb = ( ρ + у)d q

Поскольку до деформации все волокна имели одинаковую длину dz, разность отрезков аb и cd представляет собой абсолютное удлинение выделенных волокон:

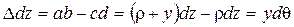
Дата добавления: 2014-01-06