Напряжения при поперечном изгибе

Лекция 9

НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ

Как уже говорилось, поперечным называют изгиб, при котором в сечении балки помимо изгибающего момента возникает поперечная сила. В этом случае в поперечных сечениях вместе с нормальными напряжениями σ появляются касательные напряжения τ. Наличие касательных напряжений вызывает сдвиг отдельных волокон относительно друг друга, и сечение, бывшее до деформации плоским, после нагружения искривляется. Это явление носит название депланации сечений (рис. 9.1, а).

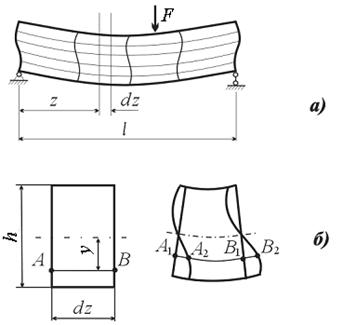
Рис. 9.1

Однако нарушение гипотезы плоских сечений практически не влияет на распределение нормальных напряжений, найденное нами при рассмотрении чистого изгиба – формулы (8.4), (8.5), (8.7) остаются справедливыми и при поперечном изгибе:

; ; .

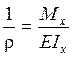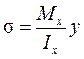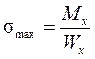Этот факт можно объяснить тем, что если поперечная сила на участке постоянна, искривление всех сечений происходит одинаково, и удлинение произвольного продольного волокна АВ (рис. 9.1, б) не зависит от того, остались ли сечения плоскими:

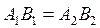
При изменяющейся поперечной силе указанные формулы дают некоторую погрешность, величина которой пропорциональна относительной высоте сечения балки h / l и в большинстве случаев незначительна. Сказанное даёт нам основания и при поперечном изгибе пользоваться гипотезой плоских сечений, считая, что картина деформаций в основном определяется поворотом сечений, а не их искривлением за счёт сдвиговых деформаций.

КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ. ФОРМУЛА ЖУРАВСКОГО

Наличие поперечной силы Q_y приводит к появлению в плоскости сечения касательных напряжений τ _zy (рис.9.2). По закону парности такие же по величине напряжения действуют в продольных сечениях:

.

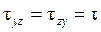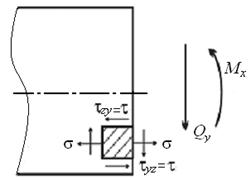
Рис. 9.2

Для нахождения касательных напряжений выделим из балки, подвергнутой поперечному изгибу, бесконечно малый элемент длиной dz, показанный на рис.9.3, а. В поперечных сечениях, образующих грани элемента, показаны нормальные и касательные напряжения, а также внутренние усилия. При этом учтено, что изгибающие моменты в левом и правом сечениях не равны друг другу и отличаются на величину dM_x в силу того, что Q_y = dM_x/dz ¹ 0. Нормальные напряжения также не будет равны, их отличие с учётом (8.5) составит величину

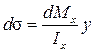
Дополнительно рассечём выделенный элемент горизонтальной плоскостью, проходящей на произвольном расстоянии y от нейтральной оси, и рассмотрим условие равновесия нижней части элемента. Площадь поперечного сечения отсечённой части элемента обозначим A _отс, положение элементарной площадки dA определим координатой y₁ (рис.9.3. б). Равнодействующая нормальных сил s dA в левом сечении равна

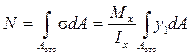(9.1)

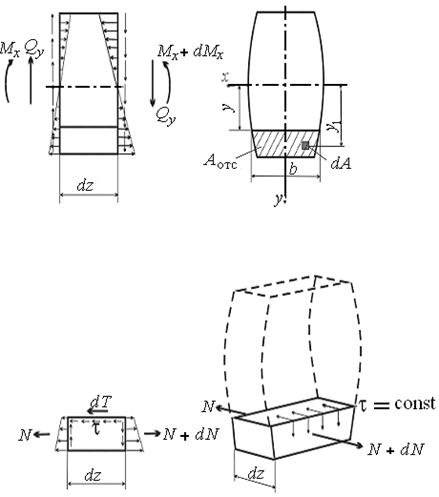
Рис. 9.3

Входящий в последнее выражение интеграл представляет собой статический момент площади A _отс относительно нейтральной оси x. Обозначив его величину 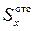, получим

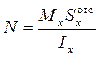. (9.2)

В правом сечении равнодействующая нормальных сил будет иной:

.

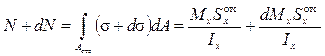Разность этих сил

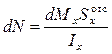(9.3)

должна в проекции на ось z уравновешиваться касательной силой dT, действующей в продольном сечении элемента (рис. 9.3, б).

Предположив, что по ширине сечения b касательные напряжения t распределены равномерно, а так же учитывая малость элемента в направлении оси балки, усилие dT можно представить следующим образом

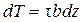. (9.5)

Из полученных зависимостей(9.3) и (9.5) с учётом равенства (9.4) получаем формулу для нахождения касательных напряжений:

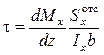. (9.6)

При отсутствии распределённой моментной нагрузки m последнее выражение принимает вид

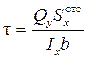. (9.7)

Таким образом, мы определили напряжения в горизонтальном сечении, проведённом на расстоянии y от нейтральной оси. По закону парности они равны напряжениям в поперечном сечении балки. Напомним, что b – ширина поперечного сечения в месте его рассечения горизонтальной плоскостью, а 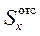- статический момент отсеченной площади A _отс относительно горизонтальной центральной оси х. Выражение (9.7) называется формулой Журавского, по имени профессора Д.И.Журавского (1821-1891гг.), впервые получившего её при разработке методов расчёта мостовых сооружений в ходе проектирования и строительства железной дороги С.Петербург – Москва в середине XIX века.

РАСПРЕДЕЛЕНИЕ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ

В БАЛКАХ РАЗЛИЧНОГО СЕЧЕНИЯ

Из величин, входящих в правую часть формулы Журавского, в общем случае функциями координаты y являются статический момент 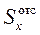и ширина сечения b. При подходе к нижней кромке сечения, площадь A _отс (рис.9.3, б) стремится к нулю, а вместе с ней обращается в нуль и статический момент 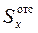. При подходе к верхней кромке площадь отсечённой части A _отс оказывается равна площади всего сечения A. Поскольку ось х является центральной, то статический момент и в этом случае равен нулю. Таким образом, касательные напряжения обращаются в нуль на верхней и нижней границах сечения. Характер их изменения внутри сечения рассмотрим на нескольких примерах.

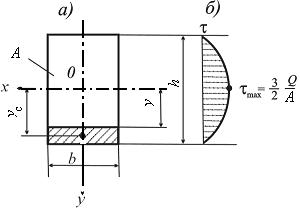
Рис. 9.4

1. Прямоугольное сечение.

Для сечения размерами b и h найдём статический момент отсеченной части площади (на рис. 9.4, а заштрихована), как произведение площади A _отс на координату её центра тяжести у_с:

Учитывая, что

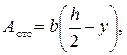
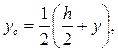
получим

.

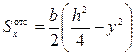Подставляя это выражение в формулу Журавского (9.7), найдём закон изменения касательного напряжения по высоте сечения:

.

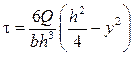Здесь принято во внимание, что для прямоугольного сечения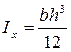

Таким образом, эпюра напряжения t, показанная на рис. 9.4, б, имеет вид квадратной параболы. Наибольшей величины напряжение достигают при значении у = 0:

.

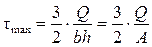Здесь A – площадь всего сечения.

2. Треугольное сечение.

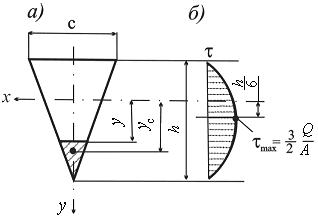
Рис. 9.5

Рассмотрим сечение треугольной формы с основанием с и высотой h (рис. 9.5, а). Обозначим ширину сечения на расстоянии y от оси как b. Тогда будем иметь:

.

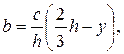
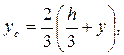
Статический элемент заштрихованной части сечения

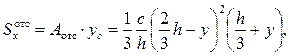
осевой момент инерции треугольного сечения

.

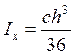Подставив полученные выражения в формулу Журавского, найдём касательное напряжение

.

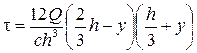Эпюра напряжений, показанная на рис. 9.5, б, как и предыдущем случае, имеет вид квадратной параболы, имеющей максимум в центральной части сечения (у = h/ 6).

Наибольшее напряжение равно

,

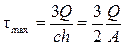где A – площадь сечения балки.

3. Круглое сечение.

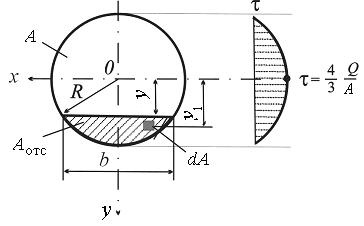
Рис. 9.6

Статический момент отсечённый части сечения, показанной на рис. 9.6 штриховкой, можно представить следующим образом

,

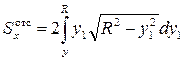где у₁ – координата, описывающая положение элементарной площадки dA.

После интегрирования получим

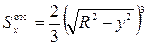
Учитывая, что для круга

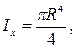
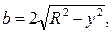
находим зависимость касательного напряжения t от вертикальной координаты у:

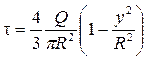
При у = 0 касательное напряжение имеет наибольшее значение

.

Эпюра t показана на рис. 9.6, б.

В двух последних примерах, строго говоря, формула Журавского не может быть признана точной. Легко показать, что здесь не выполняется допущение о постоянстве напряжений по ширине сечения.

Рассмотрим бесконечно малый элемент, в окрестности точки К сечения (рис.9.7). Пусть одна из граней элемента является частью внешней боковой поверхности балки.

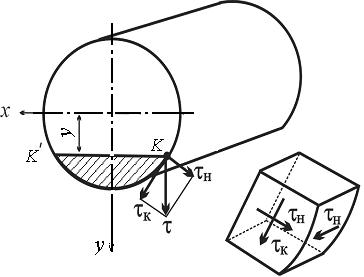
Рис. 9.7

Напряжение t в поперечном сечении всегда можно разложить на две составляющие - t_к, которая направлена по касательной к контуру сечения, и перпендикулярную ей t_н, действующую по нормали к границе сечения. По закону парности касательных напряжений, такое же по величине напряжение t_н должно действовать на перпендикулярной площадке, т.е.площадке, выходящей на боковую поверхность балки. Однако по условиям нагружения боковая поверхность должна быть свободна от сдвиговых нагрузок, следовательно,

t_н=0.

Отсюда следует вывод, что напряжение t может быть направленно только по касательной к границе сечения, т.е. совпадать со своей проекцией t_к.

В точке К^¢ напряжение t также будет направленно по касательной к контуру сечения, симметрично напряжению в точке К.

Проведённые рассуждения справедливы и для треугольного сечения, и вообще для любых сечений с плавно меняющейся толщиной. Формула Журавского в этих случаях является приближённой и позволяет вычислить не сами касательные напряжения t, а их проекцию на ось у (на плоскость нагружения).

4. Тонкостенные сечения.

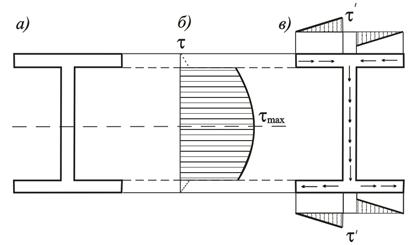
Рис. 9.8

В качестве примера тонкостенного сечения на рис. 9.8, а изображён двутавр, состоящий их двух полок и соединяющей их стойки. Такое сечение можно разбить на прямоугольники, и формально воспользовавшись формулой Журавского, получить показанные на рис. 9.8, б распределение касательных напряжений.

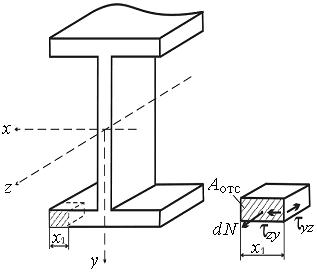
Рис.9.9

В местах соединения полок со стойкой на эпюре напряжений возникает скачок значений, связанный с резким уменьшением ширины сечения в средней части. Распределение напряжений в полках показано на эпюре пунктиром, поскольку реальная картина будет несколько иной. Дело в том, что в полках помимо вертикальных напряжений t возникают горизонтальные составляющие напряжений t ^¢, величина которых значительно больше. Если отсечь часть полки с площадью A _отс, как это показано на рис. 9.9, то нормальные напряжения приведут к появлению нормальной силы dN, подобно тому, как это описано при выводе формулы Журавского (9.7). Для обеспечения условий равновесия необходимо появление в полке касательных напряжений t ^¢:

,

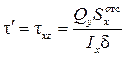где δ – толщина полки. Вдоль размера δ напряжения t _xz распределены равномерно.

По ширине полки касательные напряжения изменяются по линейному закону, поскольку

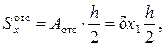
где х₁ – расстояние от края полки (см. рис. 9.9). Эпюра горизонтальных напряжений t ^¢, равномерно распределённых по толщине стенки δ и направленных по касательной к контуру сечения, показана на рис. 9.8, в. Их величина может быть найдена по формуле

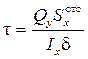(9.8)

В случае изгиба в двух плоскостях, напряжения можно найти в виде алгебраической суммы:

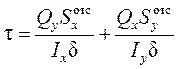(9.9)

СООТНОШЕНИЕ МЕЖДУ НАИБОЛЬШИМИ НОРМАЛЬНЫМИ И НАИБОЛЬШИМИ КАСАТЕЛЬНЫМИ НАПРЯЖЕНИЯМИ ПРИ ИЗГИБЕ

Из рассмотренных примеров следует, что зона наибольших касательных напряжений расположена в средней части высоты сечения, а величина t_max для сплошных сечений имеет порядок Q_y / A. В большинстве случаев касательные напряжения составляют по сравнению с нормальными напряжениями небольшую величину. Например, для консольной балки прямоугольного сечения, показанной на рис. 9.10

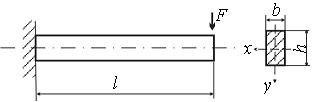
Рис. 9.10

наибольшие нормальные напряжения равны

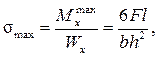
а наибольшие касательные

.

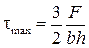Их соотношение

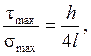
свидетельствует о том, что касательные напряжения во много раз меньше нормальных. По этой причине расчёт на прочность при поперечном изгибе, как и при чистом изгибе, производится только по нормальным напряжениям. При этом касательные напряжения во внимание не принимаются, поскольку они равны нулю в наиболее удалённых от нейтральной оси точках сечения, где максимальны нормальные напряжения.

Однако, в ряде случаев касательные напряжения при изгибе необходимо учитывать. Это относится, прежде всего, к тонкостенным профилям – двутавру, швеллеру и т.д. при нагрузках, вызывающих большую поперечную силу по сравнению с изгибающим моментом. В такой ситуации рекомендуется проводить так называемую полную проверку прочности.

Другой причиной проверки прочности по касательным напряжениям является применение изотропных материалов, плохо сопротивляющихся сдвигу – например, дерева.

ПОЛНАЯ ПРОВЕРКА ПРОЧНОСТИ ПРИ ИЗГИБЕ БАЛОК ТОНКОСТЕННОГО ПРОФИЛЯ

На рис. 9.11, а в качестве примера тонкостенного сечения изображён двутавр с обозначением характерных точек, в которых необходима проверка прочности.

В точках типа 1, наиболее удалённых от нейтральной оси, нормальные напряжения достигают максимума, а касательные равны нулю.

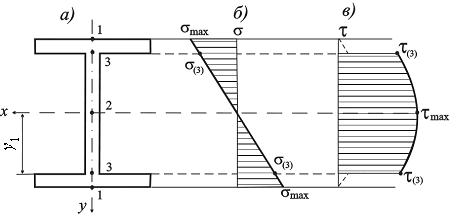
Рис. 9.11

Для тонкостенных сечений, так же как и для сплошных, расчёт на прочность начинают с проверки условия (8.7):

,

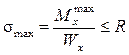что позволяет назначить размеры сечения таким образом, чтобы момент сопротивления не был меньше требуемого значения

.

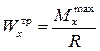Если для сплошных сечений проверка прочности на этом заканчивается, то для тонкостенных необходим дальнейший расчёт.

В опасных точках типа 2 (рис.9.11, а) возможно разрушение срезом за счёт значительных по величине касательных напряжений. Поскольку нормальных напряжений в этом месте нет, условие прочности имеет вид

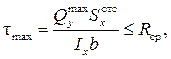(9.10)

где R _ср – расчётное сопротивление материала на срез.

Применительно к двутавровому сечению условие прочности по касательным напряжениям принимает вид

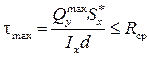(9.11)

Здесь 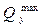- наибольшее по модулю значение поперечной силы;

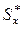- статический момент половины сечения относительно оси х (для стандартных профилей приведён в справочных таблицах);

d – толщина стойки двутавра;

Если условие прочности по касательным напряжениям не выполняется, необходимо увеличить номер стандартного профиля и повторить расчёт по формуле (9.11). Условие прочности по нормальным напряжениям при этом можно не проверять, поскольку оно заведомо выполняется.

Наконец, необходимо исключить разрушение в опасных точках типа 3, расположенных в местах перехода от полок к стенке. Здесь ни нормальные, ни касательные напряжения не достигают максимума, но имеют значительную величину и действуют совместно. Для проверки прочности в такой ситуации необходимо привлекать т.н. теории прочности, о которых речь пойдет ниже. Пока же приведём условия прочности по наиболее часто применяемым для пластичных материалов третьей и четвёртой теориям:

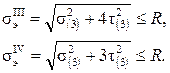(9.12)

Здесь 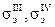- эквивалентные напряжения по соответствующим теориям прочности, 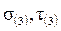- нормальное и касательное напряжение в точке 3 (рис. 9.11, а):

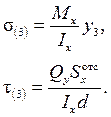
В последнюю формулу входит величина 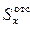, представляющая собой статический момент полки двутавра относительно оси х. Полка схематизируется в виде прямоугольника, размеры которого приведены в справочных таблицах. Статический момент этой фигуры легко вычисляется как произведение площади прямоугольника на расстояние от его центра тяжести до оси х.

Отметим, что обеспечить прочность на этом этапе расчета, необходимо для всех сечений, где одновременно велики изгибающий момент и поперечная сила.

Дата добавления: 2014-01-06