Позиционные игры с идеальной памятью

Игры с идеальной памятью являются интересным обобщением игр с полной информацией.

Определение. Игрой с идеальной памятью называется игра, в которой каждый из игроков всегда помнит все, что он делал или знал во время каждого из своих ходов.

Например, всякая игра двух игроков, в которой могут играть лишь два человека (а не команда), способные помнить всю информацию о выборах в любом ходе, является игрой с идеальной памятью. Используя понятие информационного множества, игру с идеальной памятью можно определить более точно. Позиционная игра — это игра с идеальной памятью, если для нее выполняются следующие условия: пусть 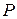и 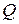— любые два хода, выполняемые одним игроком и такие, что в некоторой партии игры ход Р предшествует ходу ;

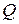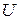и V — информационные множества, содержащие соответственно 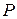и 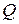; каждая точка множества 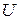дает 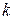альтернатив;

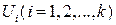— множество всех узлов дерева (ходов), которые можно достигнуть, выбрав 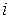-ю альтернативу в некоторой точке множества 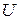, тогда для любого 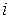имеет место соотношение .

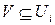Чтобы исследовать подобные игры, удобно ввести понятие стратегии поведения, состоящей в применении случайных выборов на каждом ходу игры.

Определение. Стратегией поведения данного игрока называется функция, определенная на классе информационных множеств, которая соотносит каждому информационному множеству 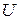элемент — набор вероятностей выбора альтернатив, т.е. из множества S, где 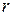— число альтернатив, которое дает 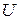. По данной стратегии поведения одного игрока и по данной чистой или смешанной стратегии или стратегии поведения другого игрока можно вычислить ожидаемый выигрыш каждого игрока.

Дата добавления: 2014-01-06