Идеальные связи, обобщенные силы

Найдем сумму работ всех сил, действующих на СМТ, на виртуальном перемещении СМТ, обозначив ее через dА. Сообщим точкам СМТ виртуальные перемещения 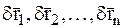и подсчитаем сумму элементарных работ, приложенных к этим МТ сил, на этих перемещениях. По аналогии с выражением суммы элементарных работ сил на действительных перемещениях работу этих сил на виртуальных перемещениях можно записать в виде:

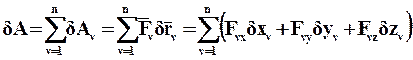. (1.11)

Определение: Сумма элементарных работ, которые могли бы совершить силы, приложенные к точкам СМТ на ее виртуальном перемещении, называется виртуальной работой.

С работой пассивных сил на виртуальных перемещениях связано понятие идеальных связей.

Определение: Связи называются идеальными, если сумма элементарных работ пассивных сил (реакций связей) на любом виртуальном перемещении равняется нулю, т.е.

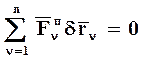. (1.12)

Для каждой из МТ, входящей в СМТ, радиус-вектор можно выразить через обобщенные координаты, которые являются функциями времени:

n=1,2,…,n (1.13)

или в проекциях на оси координат:

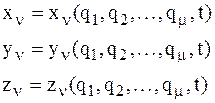n=1,2,…,n.

Найдем вариацию радиуса-вектора n-й точки СМТ:

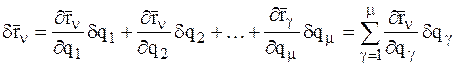. (1.14)

Подставляя эти значения 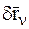в соотношение (1.11) и изменяя порядок суммирования, получим:

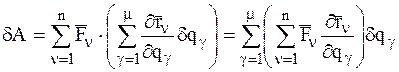. (1.15)

Введем обозначения:

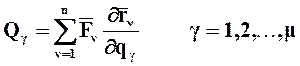. (1.16)

Тогда выражение для работы сил на виртуальных перемещениях через обобщенные координаты примет вид:

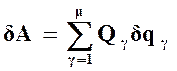. (1.17)

Эта формула по своей структуре совпадает с формулой (1.11) и исходя из этой аналогии вводится понятие обобщенных сил.

Определение: множители Q₁,Q₂,…,Q_m, стоящие в формуле (1.17) перед вариациями обобщенных координат, называются обобщенными силами, отнесенными к соответствующим обобщенным координатам.

Возможны три способа нахождения обобщенных сил:

· Обобщенные силы можно вычислить по формуле (1.16), предварительно выразив координаты МТ или точек СМТ через обобщенные координаты.

· Для вычисления обобщенных сил можно использовать формулу (1.17), определив обобщенные силы как коэффициенты при вариациях обобщенных координат в выражении суммы элементарных работ всех сил на виртуальных перемещениях. Учитывая, что вариации обобщенных координат независимы и могут принимать произвольные значения, дадим СМТ такое виртуальное перемещение, при котором вариации всех обобщенных координат, кроме одной, будут равны нулю, например, 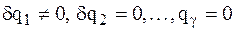, (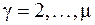). Тогда из соотношения (1.17) находим 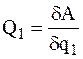, и так далее для всех обобщенных сил.

· В случае, когда СМТ находится в потенциальном силовом поле, т. е. силы являются консервативными силами, для проекций силы, приложенной к n-й точке СМТ (Ч. 3 Динамика), можно записать:

,

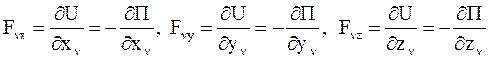где U(x,y,z) – силовая функция, а 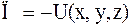– потенциальная энергия. Подставляя эти значения в соотношения (1.16) и учитывая, что П зависит от обобщенных координат сложным образом, имеем:

.

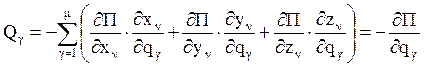При решении задач чаще всего используется второй способ.

Дата добавления: 2014-01-06