Параграф 5. Теорема о движении центра масс СМТ при ударе

Поскольку количество движения СМТ равно произведению массы CМТ на скорость центра масс СМТ (4.16), то уравнению (8.8) можно придать иную форму:

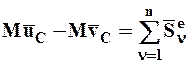, (8.10)

где М – масса СМТ, а 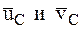– скорости центра масс СМТ в начале и в конце удара.

Уравнение (8.10) представляет выражение теоремы о движении центра масс СМТ при ударе:

Теорема: Изменение при ударе количества движения центра масс СМТ, в котором сосредоточена вся ее масса, равно геометрической сумме импульсов всех внешних ударных сил, действующих на СМТ.

Из уравнения (8.10) видно, что внутренние ударные импульсы, возникающие, например, при столкновении тел, входящих в состав данной СМТ, не изменяют скорости центра масс этой СМТ.

Проектируя обе части равенства (8.10) на координатные оси, получим:

(8.11)

Из соотношений (8.11) следует, что изменение за время удара проекции на какую-нибудь ось количества движения центра масс СМТ, в котором сосредоточена вся ее масса, равно сумме проекций на ту же ось импульсов внешних ударных сил, действующих на СМТ.

Параграф 6. Теорема об изменении кинетического момента СМТ при ударе

Рассмотрим основное уравнение теории удара для n-й МТ рассматриваемой СМТ:

.

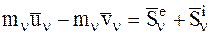Обозначим радиус-вектор n-й точки СМТ относительно начала О инерциальной системы координат через . Как было показано в пункте 8.2, положение n-й точки за время удара не изменится, а следовательно, за это время не изменится и ее радиус-вектор .

Составив такие же уравнения для всех n МТ рассматриваемой СМТ, а затем умножив обе части равенства векторно слева на радиус-вектор и сложив их почленно, получим:

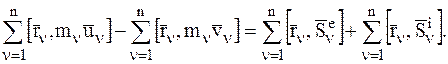
Введем следующие обозначения:

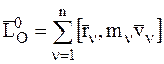– кинетический момент СМТ относительно центра О до удара,

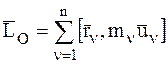– кинетический момент СМТ относительно центра О после удара.

Так как внутренние ударные импульсы равны по модулю и противоположны по направлению, то геометрическая сумма их моментов относительно любого центра равна нулю. Поэтому полученное уравнение с учетом обозначений примет вид:

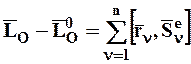
или (8.12)

.

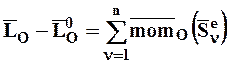Это уравнение представляет выражение теоремы об изменении кинетического момента СМТ при ударе.

Теорема: Изменение за время удара кинетического момента СМТ относительно какого-нибудь неподвижного центра равно геометрической сумме моментов импульсов внешних ударных сил, действующих на СМТ, относительно того же центра.

Проектируя соотношение (8.12) на координатные оси, получим скалярную форму теоремы об изменении кинетического момента при ударе:

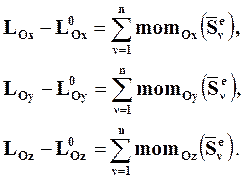(8.13)

Из соотношений (8.13) следует, что изменение за время удара кинетического момента СМТ относительно какой-либо неподвижной оси равно сумме моментов импульсов внешних ударных сил, действующих на СМТ, относительно той же оси.

Используя соотношения (8.12) и (8.13), можно получить два следствия, аналогичных двум следствиям, полученным для этой теоремы в главе 4.

Дата добавления: 2014-01-06