I. Разработка алгоритма решения

Алгоритм вычисления

Алгоритм вычисления

Алгоритм вычисления

Геометрическая интерпретация

Геометрическая интерпретация

Система уравнений

Студент Петров А.П. 1-го курса, 3 группы.

Система уравнений

Студент Петров А.П. 1-го курса, 3 группы.

Методом Зейделя

Как решить проблему входа во внешний цикл с начальными приближенными значениями корней?

Контрольное задание №4

«Решение СЛАУ методом простой итерации»

Дана:

(S+6)x+2y+3z=2

2x+(S+5)y+z=2

3x+2y+(S+4)z=2

Х0 = 0, Y0 = 0, Z0 = 0

Найти: корни системы уравнений Хk =?, Yk =?, Zk =?

методом простой итерации с погрешностью Е=0,01

Контрольное задание №5

«Решение СЛАУ методом Зейделя»

Дана:

(S+6)x+2y+3z=2

2x+(S+5)y+z=2

3x+2y+(S+4)z=2

Х0 = 0, Y0 = 0, Z0 = 0

Найти: корни системы уравнений Хk =?, Yk =?, Zk =?

методом Зейделя с погрешностью Е=0,01

левосторонней производной функции в (_*) x_i

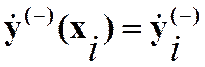
Dx_ik - k-ое приращение независимой переменной в (_*) x_i

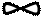Dx_ik =0,5Dx_i(k-1), то есть Dx_ik Þ 0 при kÞ

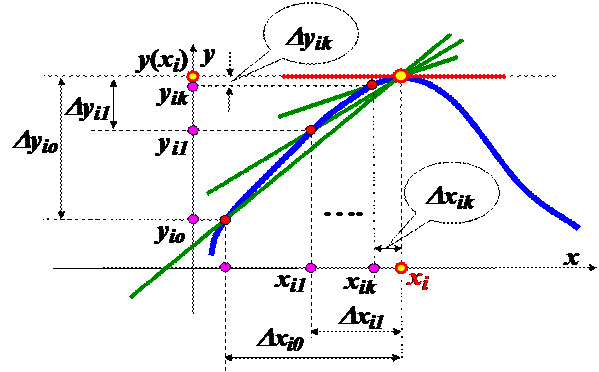
x_ik= x_i -Dx_k

у(x_ik)= у_ik

Dу_ik (x)= у(x_i) - у(x_ik)= у(x_i) - у(x_i-Dx_k)

…

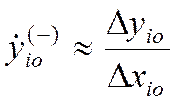
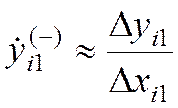
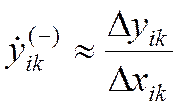
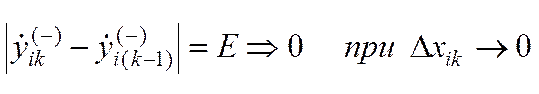
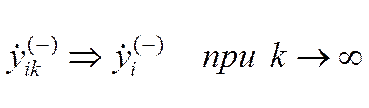
правосторонней производной функции в точке x_i

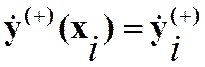
Dx_ik - k-ое приращение независимой переменной в (_*) x_i

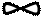Dx_ik =0,5Dx_i(k-1), то есть Dx_ik Þ 0 при kÞ

x_ik= x_i +Dx_k

у(x_ik)= у_ik

Dу_ik (x)= у(x_ik) - у(x_i) = у(x_i + Dx_k) - у(x_i)

…

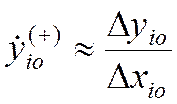
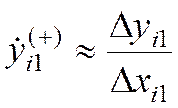
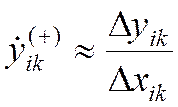
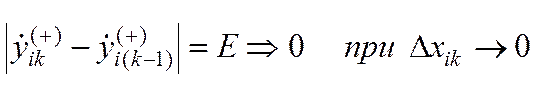
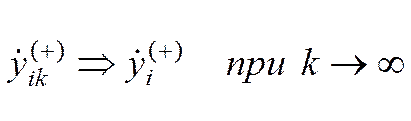
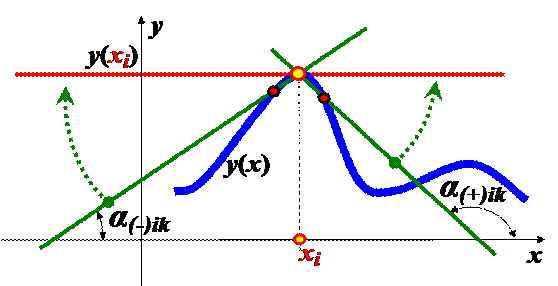
Критерий отсутствия излома графика у (х_i) в (_*) х_i

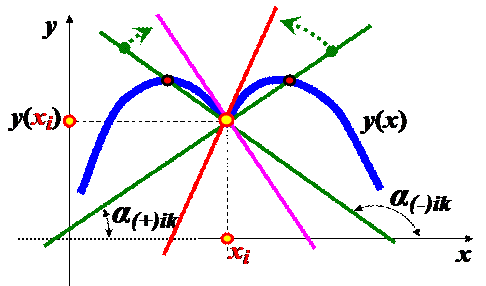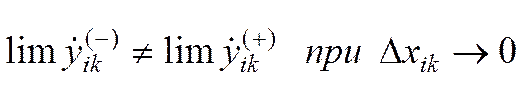
левосторонней производной функции в (_*) x_i

10) Печатать «Название и номер контрольной работы»

20) Печатать «Дата, ФИО студента»

30) Ввести числовое значение номера группы G =?

40) Ввести числовое значение номера по списку в журнале S =?

50) Ввести числовое значение заданной погрешности вычислений Е =?

60) Ввести числовое значение x_i =?

70) Ввести числовое значение k = 0

80) Ввести произвольное числовое значение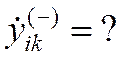

90) Вычислить у (x_i) =у_i =?

100) Ввести числовое значение D x_ik =?

110) Присвоить индексу очередное числовое значение k:= k +1

120) Уменьшить приращение D x_ik = 0,5 D x_i(k-1)

130) Вычислить у (x_ik) = у_ik = у (x_i -Dx_ik)= ?

140) Вычислить Dу (x_ik) = у_i - у_ik =?

150) Вычислить k-ое левостороннее приближение производной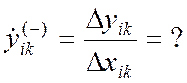

160) Проверить точность дифференцирования:

170) Принять решение: если 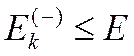, то перейти к строке 180, в ином случае, когда

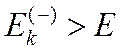, то есть погрешность велика, следует вернуться к строке 110

180) Печать приближенного значения производной «»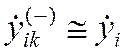

190) Завершить работу программы

правосторонней производной функции в (_*) x_i

10) Печатать «Название и номер контрольной работы»

20) Печатать «Дата, ФИО студента»

30) Ввести числовое значение номера группы G =?

40) Ввести числовое значение номера по списку в журнале S =?

50) Ввести числовое значение заданной погрешности вычислений Е =?

60) Ввести числовое значение x_i =?

70) Ввести числовое значение k = 0

80) Ввести произвольное числовое значение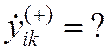

90) Вычислить у (x_i) =у_i =?

100) Ввести числовое значение D x_ik =?

110) Присвоить индексу очередное числовое значение k:= k +1

120) Уменьшить приращение D x_ik = 0,5 D x_i(k-1)

130) Вычислить у (x_ik) = у_ik = у (x_i +Dx_ik)= ?

140) Вычислить Dу (x_ik) = у_ik - у_i =?

150) Вычислить k-ое правостороннее приближение производной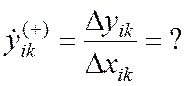

160) Проверить точность дифференцирования:

170) Принять решение: если 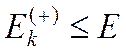, то перейти к строке 180, в ином случае, когда

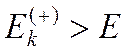, то есть погрешность велика, следует вернуться к строке 110

180) Печать приближенного значения производной «»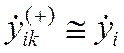

190) Завершить работу программы

производной гладкой функции в (_*) x_i

10) Печатать «Название и номер контрольной работы»

20) Печатать «Дата, ФИО студента»

30) Ввести числовое значение номера группы G =?

40) Ввести числовое значение номера по списку в журнале S =?

50) Ввести числовое значение заданной погрешности вычислений Е =?

60) Ввести числовое значение x_i =?

70) Ввести числовое значение k = 0

80) Ввести произвольное числовое значение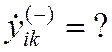

80) Ввести произвольное числовое значение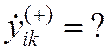

90) Вычислить у (x_i) =у_i =?

100) Ввести числовое значение D x_ik =?

110) Присвоить индексу очередное числовое значение k:= k +1

120) Уменьшить приращение D x_ik = 0,5 D x_i(k-1)

130) Вычислить у^(-) (x_ik) = у^(-)_ik = у (x_i -Dx_ik)= ?

140) Вычислить у⁽⁺⁾ (x_ik) = у⁽⁺⁾_ik = у (x_i +Dx_ik)= ?

150) Вычислить Dу^(-) (x_ik) =у_i - у^(-)_ik =?

160) Вычислить Dу⁽⁺⁾ (x_ik) = у⁽⁺⁾_ik - у_i =?

170) Вычислить k-ое левостороннее приближение производной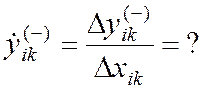

180) Вычислить k-ое правостороннее приближение производной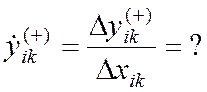

190) Проверить точность правостороннего дифференцирования:

200) Проверить точность левостороннего дифференцирования: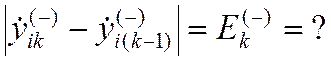

210) Проверить среднюю точность дифференцирования:

220) Принять решение: если 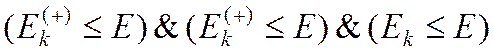, то перейти к строке 230, в ином случае, когда одна из погрешностей велика, следует вернуться к строке 110

230) Печать приближенного значения производной «»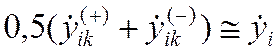

240) Завершить работу программы

Блок-схема алгоритма численного дифференцирования

(правостороннего приближения)

03.10.03 Студент Алексеев П.М. группа – 3

Контрольная работа №4

«Численное дифференцирование»

Дано:

x_i =p_/(3S); Dx_i0 =p_/(30S)  

Функция y(x) = G* sin (S*x),

где G -номер группы; S- номер студента по журналу.

Рекомендуемое начальное приближение y`_i0 = 200

Допустимая погрешность вычислений Е < 0,1

Найти:

Найти с заданной погрешностью левостороннее приближение производной функции в точке х_i или y`(х_i)=?

……..

Дата добавления: 2014-01-06