
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Изоморфизм графов
|
|
|
|
Определение 3.4.1. Графы G 1 =.(X 1,. A 1) и G 2 =.(X 2,. A 2) изоморфны ( рис.15 ), если существует взаимно однозначное соответствие между множествами вершин X 1 и X 2, такое, что любые две вершины одного графа соединены тогда и только тогда, когда соответствующие вершины соединены в другом графе.
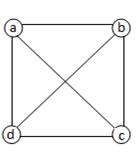
|  рис.15 рис.15
|
| G1 | G2 |
Изморфные графы рассматриваются как идентичные: их различия связаны со способом реализации, но не с внутренней структурой.
Определение 3.4.2. Инвариантом графа называется параметр, имеющий одно и то же значение для всех графов, изоморфных заданному графу. Среди самых очевидных инвариантов отметим следующие:
1. Число вершин |V|=n.
2. Число ребер |E|=m.
3. Число компонент связности.
4. Последовательность степеней, т.е.список степеней всех вершин в убывающем порядке значений.
Для решения задач изоморфизма обычно состоят в попытках показать, что два рассматриваемые графа не изоморфны. Для этого составляется список различных инвариантов в порядке, определяемом сложностью вычисления инварианта. Затем последовательно сравниваются значения параметров графов. Как только обнаруживаются два различных значения одного и того же параметра, приходят к заключению, что данные графы не изоморфны.
Множество инвариантов, которое позволило бы этой процедуре установить изоморфность графов за полиномиальное время, называется кодом графа. К сожалению, на сегодняшний день такое множество не найдено. По существу, алгоритм рассматриваемого типа сводится к сравнению кодов двух графов. Конечно, рассмотрение большого числа инвариантов увеличивает вероятность правильного заключения об изоморфизме при совпадении всех значений параметров, но в общем случае ничего не гарантирует.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 1433; Нарушение авторских прав?; Мы поможем в написании вашей работы!