
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Системы координат, применяемые в геодезии. Понятие о примоугольной системе координат Гаусса-Крюгера
|
|
|
|
Под координатами в общем смысле понимают числа, определяющие положение точки на плоскости, любой поверхности или в пространстве.
В геодезии под координатами понимают совокупность трёх чисел, определяющих положение точки земной поверхности относительно некоторой исходной поверхности.
При определении координат точек земной поверхности в геодезии применяются следующие системы координат:
- система астрономических координат;
- система геодезических координат;
- система географических координат;
- система прямоугольных координат;
- зональная система координат в проекции Гаусса-Крюгера;
- система полярных координат.
а) Система астрономических координат
В системе астрономических координат положение точки определяется на уровенной поверхности (поверхности геоида) значениями астрономических широты  и долготы
и долготы 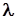 , получаемых по наблюдениям небесных светил.
, получаемых по наблюдениям небесных светил.
За начало отсчёта координат в данной системе принимают плоскость экватора ЕQ, перпендикулярную к оси вращения Земли, и плоскость начального астрономического меридиана РМ0 Р1, в качестве которого принят Гринвичский меридиан (рисунок 1. 3).
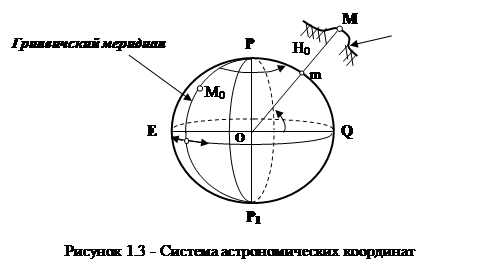 |
Астрономическая широта  - угол, образованный отвесной линией МО в данной точке и плоскостью экватора. Широты отсчитываются к северу и югу от экватора от 00 до 900. Они называются южными, если точки расположены к югу от экватора, и северными, если точки расположены к северу от него.
- угол, образованный отвесной линией МО в данной точке и плоскостью экватора. Широты отсчитываются к северу и югу от экватора от 00 до 900. Они называются южными, если точки расположены к югу от экватора, и северными, если точки расположены к северу от него.
Астрономическая долгота 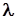 - двугранный угол между плоскостями астрономического меридиана данной точки РmР1 и начального меридиана РМ0Р1. Долготы отсчитывают в градусной мере от 00 до 1800 или в часовой от нуля до 12 часов к востоку и западу от начального меридиана и называют восточными и западными.
- двугранный угол между плоскостями астрономического меридиана данной точки РmР1 и начального меридиана РМ0Р1. Долготы отсчитывают в градусной мере от 00 до 1800 или в часовой от нуля до 12 часов к востоку и западу от начального меридиана и называют восточными и западными.
Третьей координатой в этой системе координат является ортометрическая высота Н0 - высота точки М физической поверхности Земли над поверхностью геоида (рисунок 1.3).
б). Система геодезических координат
Координатными плоскостями в этой системе координат являются плоскость экватора земного эллипсоида и плоскость Гринвичского меридиана, принятого за начальный (рисунок 1.4).
 |
Плоскость экватора ЕQ проходит через центр эллипсоида О перпендикулярно к оси вращения РР1 эллипсоида. Плоскость РmР1, проходящая через нормаль Мр к поверхности эллипсоида в данной точке М, называется плоскостью геодезического меридиана этой точки. В качестве начального меридиана принят Гринвичский меридиан. В системе геодезических координат положение точки определяется на поверхности земного эллипсоида значениями геодезической широты В, геодезической долготы L и геодезической высоты НГ .
Геодезическая широта В точки М - угол между нормалью Мр к поверхности эллипсоида в данной точке и плоскостью экватора ЕQ.
Геодезическая долгота L точки М - двугранный угол между геодезическим меридианом данной точки РМР1 и начальным РМ0 Р1, в качестве которого принят Гринвичский меридиан.
Геодезические широта и долгота отсчитываются точно так же, как и астрономические.
Геодезическая высота НГ точки М (рисунок 1.4) - расстояние по нормали от данной точки на физической поверхности до её проекции на поверхность земного эллипсоида.
в). Система географических координат
Геодезические и астрономические координаты точек имеют между собой принципиальное различие, выражающееся несовпадением поверхностей геоида и эллипсоида. Это несовпадение выражается уклонением u в данной точке отвесной линии от нормали к поверхности эллипсоида (рисунок 1.1), которое может достигать нескольких секунд дуги. Этими различиями в системах координат при выполнении высокоточных геодезических работ не пренебрегают.
При выполнении инженерно-геодезических работ, как правило, нет необходимости различать геодезические и астрономические координаты, вследствие чего пользуются более общим понятием - системой географических координат, в которой широта и долгота обозначаются соответственно  и
и 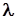 , полагая, что В =
, полагая, что В = , а L =
, а L = 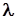 .
.
Таким образом, систему географических координат можно считать единой и обобщённой для всех точек земной поверхности, в которой уровенная поверхность принимается за поверхность шара, а за начало отсчёта координат - начальный (Гринвичский) меридиан и плоскость экватора.
В инженерной геодезии, как правило, нет необходимости различать и изложенные выше системы высот.
При решении различных инженерно-геодезических задач пользуются понятиями абсолютных, относительных и условных высот точек.
Абсолютная высот а НА точки А (рисунок 1.5) - расстояние, измеряемое от уровня моря до данной точки.
 |
Расстояние  , измеряемое от произвольной уровенной поверхности до данной точки, называется её условной высотой.
, измеряемое от произвольной уровенной поверхности до данной точки, называется её условной высотой.
Разность высот двух точек называется относительной высотой или превышением, обозначаемым через h.
В Российской Федерации высоты точек земной поверхности отсчитываются от среднего многолетнего уровня Балтийского моря. Поэтому система высот называется Балтийской.
г). Система прямоугольных координат
Система прямоугольных координат применяется для определения координат точек на сравнительно небольших участках земной поверхности. Основными координатными линиями в этой системе координат являются две взаимно перпендикулярные линии с началом в точке их пересечения О (рисунок 1.6), называемые осями абсцисс Х и ординат У.
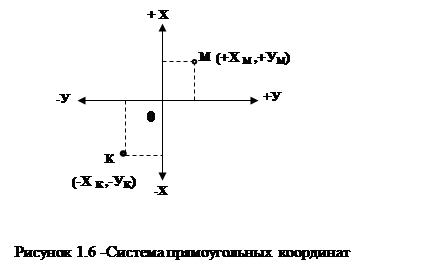 |
Северной направление оси абсцисс считается положительным (+), а южной - отрицательным (-). Направление оси ординат считается положительным к востоку и отрицательным к западу.
Оси координат делят плоскость на четыре части, называемые четвертями: I-СВ, II- ЮВ, III- ЮЗ, IV- СЗ.
Положение точки в этой системе координат определяется значениями абсциссы Х и ординаты У с соответствующим знаком в зависимости от четверти, в которой находится точка. Например, положение точки М определяется координатами +ХМ, +УМ, а точки К - координатами -ХК, -УК.
д). Зональная система координат в проекции Гаусса-Крюгера
В целях решения многообразных народно-хозяйственных задач необходимо изображать на плоскости (листе бумаги) значительные территории земной поверхности, для чего необходима проекция, обеспечивающая сохранение подобия фигур при переходе с шарообразной земной поверхности на плоскость. Возникающие при этом искажения размеров фигур должны быть малы и легко учитываться. Эти требованиям в лучшей степени удовлетворяет равноугольная поперечно-цилиндрическая проекция, предложенная К.Ф.Гауссом, математически разработанная Крюгером и принятая в нашей стране в 1928 году.
Изображение шарообразной земной поверхности на плоскости в этой проекции получают следующим образом.
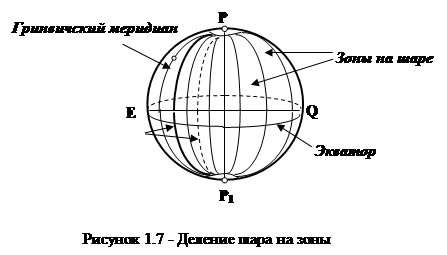
Поверхность земного шара делят меридианами на шести- или трёхградусные зоны (рисунок 1.7) и проводят внутри каждой зоны осевой меридиан. Счёт зон ведётся от Гринвичского меридиана. При делении земного шара на шестиградусные зоны их будет 60.
 |
Затем шар с нанесёнными зонами располагают внутри цилиндра таким образом, чтобы экватор ЕQ был совмещен с осью цилиндра, а осевой меридиан первой зоны - с боковой поверхностью цилиндра. Проектируют первую зону из центра шара на боковую поверхность цилиндра (рисунок 1.8).
 |
Далее перемещают шар вдоль оси цилиндра на расстояние, равное ширине зоны, поворачивают вокруг оси РР1 до совмещения осевого меридиана второй зоны с боковой поверхностью цилиндра и проектируют эту зону на цилиндр. Аналогично проектируют на цилиндр все остальные зоны.
Разрезав цилиндр по образующей АА и развернув его, получают на плоскости изображение всех зон шара, соприкасающихся между собой.
Каждая зона, изображённая на плоскости, имеет свою систему прямоугольных координат, начало которой находится в точке пересечения осевого меридиана зоны, принимаемого за ось абсцисс Х с экватором, принимаемым за ось ординат У.
Абсциссы, отсчитываемые к северу от экватора, считаются положительными, а к югу от него - отрицательными. Значения ординат отсчитываются от осевого меридиана зоны к востоку и западу. Ординаты, отсчитываемые к востоку, - положительные, к западу - отрицательные.
Так как территория Российской Федерации расположена в северном полушарии, то все абсциссы для всех точек будут положительными. Например, точка с абсциссой Х = 5234123 м находится на указанном удалении к северу от экватора.
Значения ординат - могут быть и положительными, и отрицательными. Чтобы избежать отрицательных значений ординат, ординату осевого меридиана принимают не за нуль, а за 500 км, т.е. начало отсчёта ординат искусственно переносят к западу на 500 км. Такие координаты называют преобразованными. Для того, чтобы определить в какой зоне находится точка, перед значением ординаты указывается номер зоны, а затем удаление от условного начала отсчёта в зоне. Например,точка К, имеющая ординату У=12345750, находится в 12-й зоне на удалении 345750 мот условного начала отсчёта или на удалении 154250 м к западу от осевого меридиана (345750 м - 500000 м).
Вследствие проектирования зон из центра шара на поверхность цилиндра имеют место погрешности в их изображении (на цилиндре зоны шире, чем на шаре). Кроме того, имеют место и искажения в длинах линий в зависимости от их удаления от осевого меридиана. Вследствие этого картографирование земной поверхности выполняется с некоторыми погрешностями.
Из картографии известно, что на поверхности шара длина линии S получает искажение  S, выражаемое формулой
S, выражаемое формулой

 ,
,
где Уm - среднее значение ординат начальной и конечной точек линии;
R - радиус Земли (R=6371 км).
S - длина измеряемой линии.
Полагая, что наибольшее значение Уm = 250 км, R=6371 км, ошибка в измеренной линии  S не превысит 50 см при длине S =500 м. Это позволяет утверждать, что картографирование в проекции Гаусса осуществляется с искажениями, практически не влияющими на точность изображения местности на карте.
S не превысит 50 см при длине S =500 м. Это позволяет утверждать, что картографирование в проекции Гаусса осуществляется с искажениями, практически не влияющими на точность изображения местности на карте.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 1912; Нарушение авторских прав?; Мы поможем в написании вашей работы!