Модель атома Бора

Развитию представлений об атоме, помимо экспериментов и модели атома, предложенной Резерфордом, способствовал анализ спектров излучения, которые испускают разреженные газы (их линейчатый или дискретный характер).

Анализ атомных спектров. Известно, что нагретые тела излучают свет с непрерывным спектром, когда зависимость интенсивности излучения от частоты описывается непрерывной функцией. Предполагалось, что это излучение обусловлено колебаниями атомов и молекул, которые зависят в основном от взаимодействия каждого атома или молекулы со своими соседями. Разреженные газы можно также «заставить» испускать свет. Для этого их необходимо возбудить, например, с использованием напряжения приложенного таким образом, чтобы разреженный газ оказался между электродами. Было обнаружено, что спектр излучения разреженных газов является не непрерывным, а дискретным. Так как возбужденные газы испускают свет только определенных длин волн, в спектроскопе или спектрометре наблюдается не непрерывный, а линейчатый спектр. Каждое вещество обладает своим, характерным только для него спектром испускания (набором частот, на которых происходит поглощение или испускание света данным видом атомов или молекул). Спектр служит своего рода «отпечатком пальцев», позволяющим идентифицировать состав вещества[10].

Водород представляет собой простейший атом: вокруг ядра обращается только один электрон. У атома водорода самый простой спектр. На рис.12.7 представлен линейчатый спектр атома водорода.

Рис. 12.7. Линейчатый спектр атомарного водорода..

Если линия имеет цвет, то при данной частоте, а, следовательно, и энергии, атом излучает. Если линия спектра черная, то на этой частоте происходит поглощение излучения.

В 1885 г. Дж.Дж. Бальмер показал, что четыре видимые линии в спектре водорода связаны между собой эмпирическим соотношением:

(12.4.1)

где R – постоянная Ридберга ().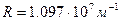

Формула Бальмера справедлива и для спектральных линий, соответствующих большим целочисленным значениям п. Впоследствии было обнаружено, что спектральные линии серии Бальмера продолжаются в ультрафиолетовой (УФ) области и заканчиваются при l=365 нм (это соответствует n ≈ ∞).

Исследования спектра водорода, выполненные несколько позже, показали, что в ультрафиолетовой и инфракрасной (ИК) областях спектра имеются другие серии линий, аналогичные по своей структуре серии Бальмера, но с другими длинами волн.

Например, в ультрафиолетовой области спектра атома водорода находится серия Лаймана:

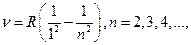(12.4.2)

В инфракрасной области спектра атома водорода оказались расположенными три серии спектральных линий:

серия Пашена:

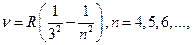(12.4.3)

серия Брэкета:

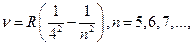(12.4.4)

серия Пфунда:

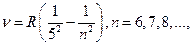(12.4.5)

Шведский ученый Ридберг[11] объединил вышеперечисленные формулы в одну общую формулу:

(12.4.6)

которая получила название обобщенной формулы Бальмера - Ридберга. В ней i – целое число, каждое значение которого соответствует определенной спектральной серии, упомянутой выше (например, i=3 соответствует серии Пашена). Эта формула представляла какую-то фундаментальную закономерность в микромире, которая в то время не могла быть объяснена.

Постулаты Бора. В 1913 году датский физик Нильс Бор[12] показал, что несовпадение с экспериментом выводов, основанных на модели Резерфорда, возникло не потому, что планетарная модель строения атома не верна. Он предположил, что в микромире физические величины принимают дискретные значения, то есть квантуются (таким образом, законы микромира - это квантовые законы). В основу своей теории он положил следующие постулаты.

1. В атоме существуют стационарные (не изменяющиеся со временем) состояния, характеризующиеся определенными дискретными (квантовыми) значениями энергии, находясь в которых атом не излучает энергию.

Стационарным состояниям атома соответствуют стационарные орбиты, по которым движутся электроны. Движение электронов по стационарным орбитам не сопровождается излучением.

2. В стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь дискретные квантованные значения момента импульса, удовлетворяющие уравнению:

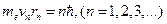(12.4.7)

где n – квантовое число орбиты или главное квантовое число, ν_n – скорость электрона, находящегося на n-ой орбите атома, r_n - радиус n-ой орбиты.

3. При переходе электрона с одной орбиты на другую излучается (поглощается) один фотон с энергией, равной разности энергий соответствующих стационарных состояний:

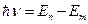(12.4.8)

Описание атома водорода в рамках модели Бора. Набор возможных дискретных частот квантовых переходов определяет линейчатый дискретный спектр атома.

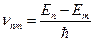(12.4.9)

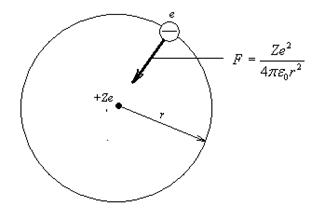
Рис.12.8. Модель атома водорода.

Вычислим радиус п -ой стационарной орбиты, используя второй закон Ньютона для описания движения электрона вокруг ядра атома по круговой орбите (рис.12.8):

F=ma, (12.4.10)

где 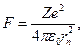– сила кулоновского взаимодействия между электроном и ядром, а 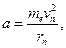– центростремительное ускорение. Второе уравнение системы представляет постулат Бора 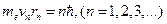. Таким образом, система из двух уравнений базируется на законах классической и квантовой механики:

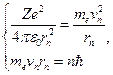(12.4.11)

Решая систему уравнений (12.4.11), находим радиусы стационарных орбит:

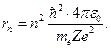(12.4.12)

Из выражения (12.4.12) численное значение радиуса первой боровской орбиты атома водорода (Z=1):

(12.4.13)

Радиусы более далеких от ядра орбит возрастают как n²:

r₂=4r₁=2.11·10^-10м, (12.4.14)

r₃=9r₁=4.74·10^-10м (12.4.15)

Полная энергия электрона в водородоподобной системе складывается из его кинетической и потенциальной энергии в электростатическом поле ядра:

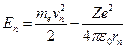(12.4.16)

Но тогда, используя первое уравнение из системы уравнений (12.4.11), получим:

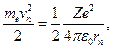(12.4.17)

значения энергии п- ой стационарной орбиты атома водорода составляют:

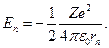(12.4.18)

Учитывая квантованные значения радиуса п- ой стационарной орбиты (12.4.12), получаем:

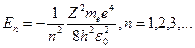(12.4.19)

(знак минус означает, что электрон находится в связанном состоянии и для того, чтобы его оторвать от атома, ему необходимо сообщить такую энергию, при которой его полная энергия станет больше нуля). Для атома водорода (Z=1) низший энергетический уровень соответствует n=1. При подстановке в формулу (12.4.19) численных значений найдем величину Е₁:

Е₁=-2.17·10^-18Дж=13.6 эВ, (12.4.20)

а энергии более высоких уровней составляют:

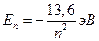(12.4.21)

При различных целых значениях п энергетические уровни схематически представлены на рис. 12.9.

Электронам, связанным в атоме соответствует энергия Е<0. Чтобы в этом случае оторвать электрон от атома необходимо затратить энергию, которая называется энергией связи или энергией ионизации атома. Свободный электрон, который не связан с атомом, имеет энергию связи Е=0. Для атома водорода энергия ионизации с низшего состояния Е₁=-13.6 эВ.

Низший энергетический уровень или состояние имеет энергию Е₁ и называется основным состоянием. Более высокие состояния (Е₂, Е₃ и т.д.) называются возбужденными состояниями. Электрон может находиться на любом из энергетических уровней, но никогда не может оказаться между ними. При комнатной температуре почти все атомы находятся в основном состоянии. С ростом температуры, в результате столкновений с большими скоростями, они переходят в возбужденные состояния. Возвращаясь обратно в основное состояние, они испускают фотон. Излучение света происходит и при переходе атома с высоко возбужденных состояний на основное или низко возбужденные состояния. Подставляя значения энергий этих уровней из (12.4.19) во второй постулат Бора, получаем:

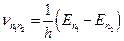, (12.4.22)

Всевозможные частоты, с которыми испускаются кванты света, определяются выражением:

, (12.4.23)

Набор этих частот создают спектр излучения атома водорода. На рис.12.9 видно, что если электроны возвращаются из различных возбужденных состояний в основное, то возникает серия Лаймана (n=1), если атомы переходят из высоковозбужденных состояний в первое возбужденное состояние (n=2), то в спектре наблюдается серия линий Бальмера, во второе – серия Пашена и т.д.

Из выражения (12.4.23) видно, что постоянная Ридберга имеет вид:

,

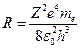а ее вычисленное значение совпадает с результатами выполненных измерений спектра атома водорода.

Модель Бора позволяет получить правильные результаты не только для атома водорода, но и в случае водородоподобных ионов, в которых вокруг ядра вращается один электрон (это, например, однозарядный ион гелия Не⁺ или лития Li⁺⁺).

Выдающийся успех теории Бора состоит в том, что она давала модель, позволяющую объяснить, почему атомы испускают линейчатые спектры, и точно предсказать для атома водорода длины волн испускаемого излучения. Теория Бора гарантировала также стабильность атомов: основное состояние является низшим энергетическим состоянием электрона и не существует более низкого энергетического уровня, на который электрон мог бы перейти из основного состояния с испусканием излучения. Она предсказала энергию ионизации атома водорода - 13.6 эВ.

а) б)

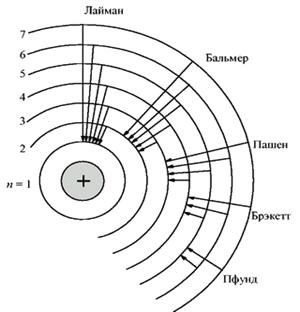
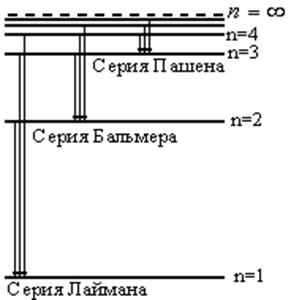
Рис.12.9. Объяснение серий линий Лаймана, Бальмера, Пашена и др. на основе модели Бора.

Недостатком же этой теории является тот факт, что она оказалась справедлива только для атома водорода и водородоподобных ионов, а спектры более сложных атомов (например, гелия) и молекул она не объясняла. Не получили объяснение и межатомные связи в молекулах, твердых телах и жидкостях. К тому же в ней существует внутренняя противоречивость, поскольку совмещались методы расчета, основанные на законах классической механики и электродинамики, с квантовыми представлениями, введенными в классическую теорию как постулаты. Не обеспечивала она и учет проблемы корпускулярно – волнового дуализма. Несмотря на недостатки, теория Бора стала переходным этапом от классических представлений о строении материи к квантовым. Она была и остается знаменательной вехой в истории науки.

Дата добавления: 2014-01-06