Квантомеханическая картина строения атома

В атоме, согласно квантовой механике, не существует вполне определенных круговых орбит электронов, как в теории Бора. В силу волновой природы электрон «размазан» в пространстве, подобно «облаку» отрицательного заряда. Размеры и форму электронного облака в заданном состоянии атома можно вычислить, решая уравнение Шредингера (13.2.9) для случая, когда атом представляет собой гармонический осциллятор. В этом случае волновая функция основного состояния атома водорода имеет вид:

, (13.4.1)

где - волновая функция, описывающая положение электрона в атоме, которая зависит от расстояния до центра и не зависит от угловых координат и времени, а постоянная совпадает с радиусом первой боровской орбиты атома водорода. Видно, что электронное облако в основном состоянии водорода сферически - симметрично, как показано на рис.13.4.

Рис.13.4. Электронное облако (распределение вероятности) для атома водорода.

Электронное облако можно интерпретировать как с корпускулярной, так и с волновой точек зрения. Под частицей мы понимаем нечто локализованное в пространстве: в любой момент времени частица занимает вполне определенное положение в пространстве. Волна же размыта в пространстве. Следовательно, размытое в пространстве электронное облако хорошо интерпретируется с точки зрения волновой природы электронов. Электронное облако можно также интерпретировать как распределение вероятности нахождения в пространстве данной частицы.

Невозможно предсказать траектории, по которой будет двигаться электрон. Можно лишь вычислить вероятность, с которой можно обнаружить электрон в различных точках.

Ясно, что подобная ситуация в корне отличается от классической ньютоновской физики. Как отмечал впоследствии Бор, при испускании атомом светового фотона, бессмысленно даже спрашивать, как электрон переходит из одного состояния в другое.

Квантовый осциллятор. Как уже отмечалось выше, атом может быть представлен в виде гармонического осциллятора, когда электрон и ион совершают колебания друг относительно друга. Эта простейшая модель атома - аналог диполя, который подробно рассматривался в лекции №8. Такой гармонический осциллятор называют квантовым осциллятором.

В этом случае уравнение Шредингера (13.2.9) представимо в нестационарной форме:

, (13.4.2)

где величина Н:

(13.4.3)

носит название оператора[4] Гамильтона.

По смыслу уравнения (13.2.7) и (13.4.2) совпадают, если в правой части (13.2.7) собрать в скобки выражение, преобразующее волновую функцию . Только выражение в виде (13.2.7) является одномерным случаем выражения (13.4.3).

Для стационарных волновых функций (когда волновая функция не зависит от времени) состояний 1s² и 2s¹ уравнение Шредингера имеет вид:

Hψ₀=Eψ₀., (13.4.4)

где Е – собственные значения оператора Гамильтона или энергия уровней в зависимости от значения главного квантового числа, ψ₀ – волновая функция.

Для гармонического осциллятора оператор U имеет форму кулоновского потенциала:

U=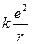, (13.4.5)

где .

В этом случае значения энергии уровней осциллятора, рассчитанные из уравнения (13.4.4), зависят от главного квантового числа n и соответственно составляют:

Е=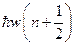 (13.4.6)

где w – собственная частота колебаний гармонического осциллятора в основном состоянии. Нарис.13.5 представлена схема уровней квантового гармонического осциллятора.

Энергия основного и первого уровня согласно (13.4.7) соответственно составляют:

Е₀=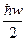, Е₁=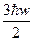. (13.4.8)

Расстояние между любыми двумя уровнями представляет собой постоянную величину, которую называют энергетической щелью.

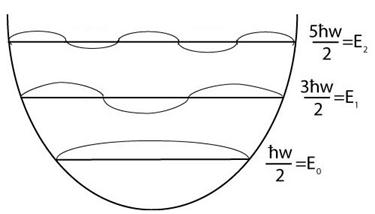
Рис. 13.5. Энергия уровней квантового гармонического осциллятора.

Дата добавления: 2014-01-06