
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Ускорение
|
|
|
|
Скорость. Средняя и мгновенная скорость.
Движение материальной точки с помощью кинематического закона может быть полностью описано.
Движение тела может быть равномерным (тело за равные промежутки времени проходит равные расстояния) или равноускоренным. Для описания равномерного движения вводится понятие скорости. Существует понятие путевой скорости V – отношения пройденного пути s к времени t, за которое пройден этот путь:
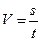 , (2.1.1)
, (2.1.1)
скорости по перемещению 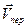 или средней скорости (отношение перемещения
или средней скорости (отношение перемещения 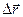 к времени):
к времени):
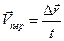 , (2.1.2)
, (2.1.2)
а также мгновенной скорости:
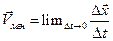 . (2.1.3)
. (2.1.3)
где 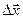 - перемещение тела за промежуток времени
- перемещение тела за промежуток времени 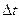 , стремящийся к нулю.
, стремящийся к нулю.
Мгновенная скорость - это скорость в данной точке, например, когда человек смотрит на спидометр автомобиля. По смыслу мгновенная скорость – это предел, к которому стремится отношение перемещения к промежутку времени при уменьшении этого промежутка до нуля (рис.2.4). Понятие мгновенной скорости представляет собой математическое понятие производной функции. Наряду с площадями сложных фигур стремление найти способ вычисления скорости движения тела в данный момент времени стало основой развития дифференциального и интегрального исчисления.
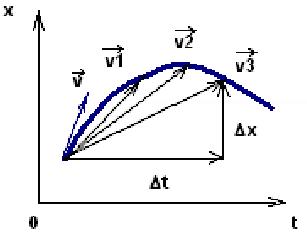
Рис.2.4. Иллюстрация к понятию мгновенной скорости 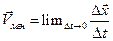 .
.
Путевая и средняя скорость различаются между собой тем, что путевая скорость всегда не меньше средней скорости. Например, если тело вернулось назад, то средняя скорость тела на всем участке пути будет равна нулю, а путевая - нет.
Скорость по перемещению по смыслу означает, если, например, расстояние между двумя пунктами преодолевается по извилистой дороге, то пройденный путь будет больше перемещения (например, расстояния между двумя населенными пунктами, измеренное линейкой на карте). Следовательно, и путевая скорость будет выше скорости по перемещению. Когда автомобиль, проехав по любой траектории, вернулся в исходную точку, его перемещение будет равно нулю
Аналогично понятиям скорости вводятся и понятие ускорения. Только в данном случае вместо пути и перемещения необходимо взять изменение скорости. Определения среднего и мгновенного ускорения вводятся по аналогии с понятиями средней и мгновенной скорости.
Среднее ускорение определяется как отношение изменения скорости к промежутку времени, в течение которого это изменение происходит:
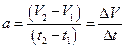 , (2.1.4)
, (2.1.4)
а мгновенное ускорение также как и мгновенная скорость, представляет ускорение в данный момент времени:
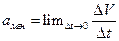 (2.1.5)
(2.1.5)
Ускорение можно представить через изменение координаты х=х(t). В этом случае оно представляет собой вторую производную зависимости координаты от времени x(t):
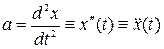 (2.1.6)
(2.1.6)
Скорость равноускоренного движения из определения ускорения (1.5) имеет вид:
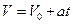 (2.1.7)
(2.1.7)
Уравнение для пути равноускоренного движения для случая, когда движение точки происходит из начала координат, определяется следующим образом:
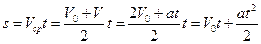 (2.1.8)
(2.1.8)
В выражении (1.17) путь s представляет собой площадь трапеции с основанием 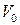 и
и 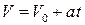 , высотой, равной времени
, высотой, равной времени 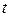 . Это наглядно видно на рис. 2.5, где представлена зависимость скорости равноускоренного движения от времени.
. Это наглядно видно на рис. 2.5, где представлена зависимость скорости равноускоренного движения от времени.
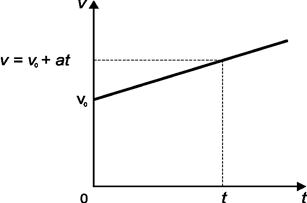
Рис.2.5. Скорость при равноускоренном движении.
Для вычисления пути можно использовать и интегральное исчисление:

|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 820; Нарушение авторских прав?; Мы поможем в написании вашей работы!