Движение точки по окружности. Векторы угловой скорости и углового ускорения

Понятие о материальной точке. Системы отсчета. Радиус-вектор. Векторы перемещения, скорости, ускорения. Траектория движения. Пройденный путь. Перемещение и путь при равномерном и равноускоренном движении.

Что такое движение и как его описывать? На этот вопрос отвечает кинематика, описывающая движение тел. Движение — это перемещение тела относительно других тел (изменение его положения в пространстве). Таким образом, описывая движение тела, мы всегда привязываемся к какой-то координатной системе, относительно которой тело движется ² , или к системе отсчета. Движение тела определяется движением всех его точек (маленьких кусочков тела), поэтому мы начнем с описания движения материальной точки.

Матеpиальной точкой называется тело, pазмеpами котоpого можно пpенебpечь, считая, что вся масса тела сосpедоточена в одной точке.

Прежде всего, выберем систему координат. Самая простая система — это декартова система координат, три взаимно перпендикулярных оси x, y, z. Различают два вида координатных систем: правую и левую (pис. 1).

Рис. 1. Правая и левая декартовы системы координат.

Никаким пространственным поворотом их нельзя совместить друг с другом, как нельзя вложить правую перчатку в левую. Но если перчатку вывернуть, то последнее оказывается возможным. Так и левая система переходит в правую при изменении направления одной из осей, например оси x, на противоположное (x → – x) (pис. 2).

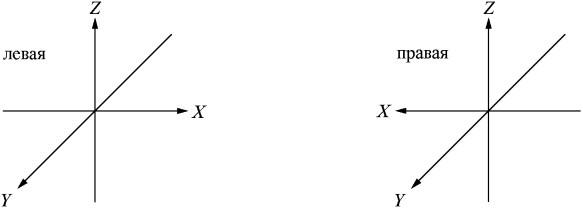Рис. 2. Переход левой системы координат в правую при изменении знака одной из осей x → – x.

После этого обе системы можно совместить взаимным поворотом и перемещением в пространстве. Такая операция (замена x → – x) называется зеркальным отражением. И именно поэтому левая система координат в зеркале кажется правой.

Левая система координат переходит в правую также и при изменении направления всех трех координатных осей (x → – x, y → – y, z → – z)

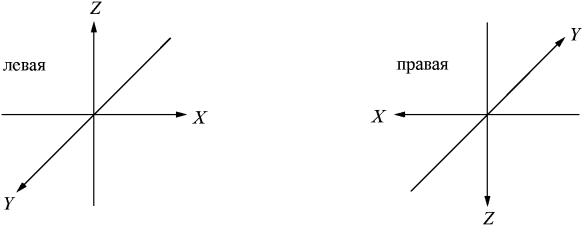Рис. 3. Операция инверсии.

с последующим поворотом. Такая операция (изменение знака всех трех осей) называется инверсией (см. pис. 3).

Законы природы, очевидно, должны быть записаны в форме, которая не зависит от выбора системы координат. Мы для определенности будем пользоваться правой системой. Положение точки в выбранной нами системе координат задается радиус-вектором ³ r, проекции которого на оси координат равны соответственно x, y, z.

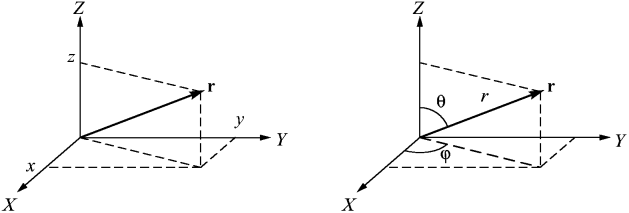Рис. 4. Радиус-вектор в декартовой и сфеpической системах координат.

Таким образом, вектор r вполне однозначно определяется заданием трех его проекций, хотя это могут быть и другие три числа, например длина r и два угла θ и φ (так называемая сферическая система координат) (pис. 4). Декартовы координаты со сферическими связаны друг с другом соотношениями

(2)

Если ввести три единичных вектора i, j, k, направленные вдоль координатных осей (единичные орты), то радиус-вектор r можно представить в виде суммы трех векторов:

r = xi + yj + zk, | i | = | j | = | k | = 1.

(3)

Это следует из известного еще в школе закона сложения векторов по правилу параллелограмма (pис. 5).

Рис. 5. Разложение радиус-вектора на составляющие вдоль координатных осей.

Длину вектора r можно найти, скаляpно умножив его на себя самого. Вы знаете еще со школьных времен, что скалярным произведением двух векторов A и B называется число

(4)

равное произведению длин векторов на косинус угла между ними. Очевидно, что если два вектора перпендикулярны друг другу, то их скалярное произведение равно нулю. Скалярное произведение радиус вектора r на себя самого равно

(5)

так как 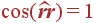(угол равен нулю). С другой стороны,

r · r	=	(xi + yj + zk)· (xi + yj + zk) =
	=	x ^2 i · i + y ^2 j · j + z ^2 k · k + 2 xyi · j +	(6)
	+	2 xzi · k + 2 yzj · k.

Но в силу взаимной ортогональности векторов i, j и k их скалярные произведения равны нулю,

i · j = i · k = j · k = 0.

(7)

В итоге мы приходим к известному результату, что квадрат длины вектора равен сумме квадратов его проекций:

r ^2 = x ^2+ y ^2+ z ^2.

(8)

Аналогичным образом может быть доказано равенство

A · B = AxBx + AyBy + AzBz.

(9)

Это легко сделать, если представить каждый из векторов в виде

A = Axi + Ayj + Azk

(10)

и аналогично для вектора B. После этого остается только их скалярно перемножить и воспользоваться равенствами (7).

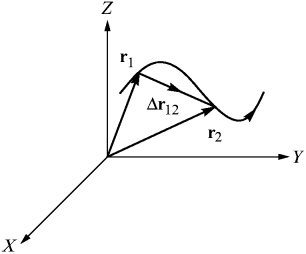Рис. 6. Траектория и перемещение материальной точки.

Рассмотрим теперь движение материальной точки, траектория которой изображена на рис. 6, и определим такие важные для дальнейшего понятия, как скорость материальной точки v и ускорение a. Пусть радиус-вектор материальной точки в момент времени t ₁ равен r ₁, а в момент времени t ₂ равен r ₂. Таким образом, при движении радиус-вектор r изменяется со временем, иными словами, он является функцией времени r = r (t). Если нам известен закон этого изменения, то мы знаем, где в каждый момент времени находится материальная точка, то есть мы знаем закон ее движения. Задание функции r (t) эквивалентно заданию трех функций x (t), y (t) и z (t) — координат материальной точки, поскольку

r (t) = x (t) i + y (t) j + z (t) k.

(11)

Разность векторов r ₂ и r ₁

Δr 12 = r 2– r 1

(12)

называется перемещением материальной точки. Очевидно, что это тоже вектор и он направлен из точки 1 в точку 2. Ясно, что

r 1+ Δr 12 = r 1+ (r 2– r 1) = r 2,

(13)

и вы узнаете известное еще в школе правило треугольника для сложения векторов. Отношение перемещения материальной точки Δ r ₁₂ к интервалу времени Δ t ₁₂ = t ₂– t ₁, то есть Δ r ₁₂ / Δ t ₁₂, тоже является вектором, причем коллинеарным вектору перемещения.

Очевидно, что если мы будем уменьшать величину интервала Δ t ₁₂ (приближая t ₂ к t ₁), то соответственно будет уменьшаться и длина вектора Δ r ₁₂, то есть величина перемещения. Предел отношения перемещения Δ r ₁₂ к интервалу Δ t ₁₂, когда последний стремится к нулю, называют производной вектора r (t) по времени t:

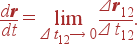
(14)

Этот вектор направлен по касательной к траектории материальной точки в точке t ₁. По определению, скорость материальной точки равна

(15)

Рис. 7. Скорость материальной точки.

Это, очевидно, вектор, направленный по касательной к траектории в точке, соответствующей моменту времени t, с компонентами

v	=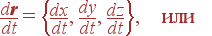
v	=		(16)
υx	=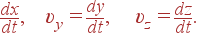

Вектор скорости частицы v (t) так же, как и радиус-вектор, является функцией времени t. Аналогичным образом можно определить вектор, характеризующий скорость изменения скорости частицы и называемый ускорением:

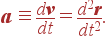
(17)

Если величина и направление этого вектора не изменяются со временем, то есть если

a = const,

(18)

то такое движение называется равноускоренным (равнозамедленным). Для равноускоренного движения скорость материальной точки v (t) и ее радиус-вектор r (t) изменяются со временем по закону

v (t)	=	v (0)+ at,
r (t)	=		(19)

где v (0) и r (0) — соответственно скорость и радиус-вектор материальной точки в начальный момент времени t = 0 (проверка дифференцированием). Траекторией точки при равноускоренном движении является, как известно, парабола ⁴ . Частным случаем равноускоренного движения является движение с ускорением, равным нулю. Такое движение называется равномерным. Очевидно, что оно происходит по прямой.

Рассмотрим теперь вопрос, как найти путь ⁵ , проходимый материальной точкой при ее движении. Рассмотрим произвольного вида траекторию, по которой движется материальная точка.

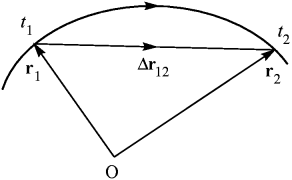Рис. 8. Как найти путь?

Пусть в момент времени t ₁ материальная точка занимала положение на траектории, характеризуемое радиус-вектором r ₁, а в момент времени t ₂ — радиус-вектором r ₂, см. pис. 8. Спрашивается, какой путь прошла материальная точка между этими двумя положениями. Перемещение материальной точки определяется вектором Δ r ₁₂ = r ₂– r ₁, но длина этого вектора, очевидно, не определяет пройденный материальной точкой путь, за исключением того случая, когда траектория материальной точки между двумя положениями представляет собой прямую линию. Это подсказывает способ нахождения пути при криволинейном движении. Для этого разобьем временной интервал t ₂– t ₁ на много одинаковых интервалов очень малой продолжительности Δ t, так что в каждом таком малом интервале движение практически прямолинейное (pис. 9). Число таких интервалов pавно

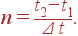
(20)

Изобразим векторы перемещения материальной точки Δ r _i (i = 1,2,..., n) в каждом из этих интервалов времени.

Рис. 9. Способ нахождения пути при криволинейном движении.

Очевидно, что при достаточно малом Δ t пройденный путь S может быть аппроксимирован суммой длин этих векторов:

(21)

По мере стремления Δ t к нулю это приближение становится все лучше и лучше и в конце концов при бесконечном n обращается в точное равенство.

Разделим и домножим каждое слагаемое в этой сумме на Δ t:

(22)

Как мы уже сказали, точное равенство получается в пределе Δ t → 0:

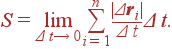
(23)

Очевидно, можно поменять местами операции суммирования и предельного перехода (предел суммы равен сумме пределов) и вспомнить, что предел

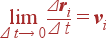
(24)

равен скорости частицы v в i –том интервале. Тогда путь может быть представлен в виде суммы бесконечного числа бесконечно малых слагаемых:

(25)

Такая операция в математике называется вычислением определенного интеграла. Напомним, что существует еще и неопределенный интеграл. Так, для некоторой функции f (t)

(26)

где dF / dt = f (t), и функция F (t) называется первообразной по отношению к f (t). Определенный интеграл в пределах от t ₁ до t ₂ от функции f (t) вычисляется при этом по правилу:

(27)

Это разность значений первообразной на верхнем и нижнем пределах.

Таким образом, мы пришли к такому результату, что

путь, пройденный частицей в интервале ее движения от t ₁ до t ₂, равен определенному интегралу по времени в этих пределах от модуля скорости частицы.

¹Такого же порядка скорость точки на поверхности Земли при ее вращении вокруг своей оси (≈ 470 м/с).

²Например, сидя в вагоне едущего поезда, мы не движемся относительно вагона, но вместе с ним движемся относительно Земли и т.д.

³В школьном курсе физики вектор — это физическая величина, характеризуемая своей длиной и направлением в пространстве. Сложение векторов осуществляется по правилу параллелограмма.

⁴В частных случаях эта парабола может вырождаться в отрезок прямой.

⁵ То есть длину траектории частицы.

Лекция 3

При равноускоренном движении частица движется все время в одной плоскости, образуемой начальным вектором скорости v (0) и постоянным ускорением a (докажите это). Однако очевидно, что далеко не всякое плоское движение является равноускоренным. Пример плоского неравноускоренного движения, известный вам из школьного курса физики, — это равномерное движение по окружности. Давайте рассмотрим его здесь. Поскольку это движение плоское, выберем в качестве этой плоскости, плоскость XY. Начало координат выберем в центре окружности (pис. 1).

Рис. 1. Равномерное движение по окружности.

Координаты частицы выразим через величину радиуса окружности r и угол α:

(1)

Поскольку движение происходит по окружности, r от времени не зависит. Функцией времени является только угол α (t). Производная от угла по времени называется угловой скоростью вращения ω:

(2)

При равномерном вращении по окружности ω = const и можно проинтегрировать это уравнение. В результате

α = ω t + const.

(3)

Константа интегрирования выбирается из условия α (0) = 0. Таким образом,

(4)

Это полностью определяет движение. Так, скорость материальной точки определяется производными по времени от координат:

υx	=
υy	=		(5)

Скалярное произведение pавно

r · v	=	xυx + yυy = r cos ω t (– ω r sin ω t)+
	+	r sin ω t (ω r cos ω t) = 0,	(6)

что означает перпендикулярность векторов r и v, то есть скорость действительно направлена по касательной к окружности. Абсолютная величина скорости равна

υ = | v |	=
	=	ω r = const,	(7)

она не зависит от времени, движение действительно равномерное (но по окружности).

Дифференцируя по времени скорость, мы можем определить ускорение:

ax	=
ay	=		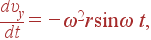(8)

откуда следует, что ускорение зависит от времени, то есть движение не является равноускоренным. Абсолютная величина ускорения (модуль), тем не менее, остается постоянной:

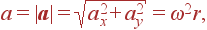
(9)

или, так как ω r = υ, то мы получаем

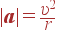
(10)

— известную из школьного курса физики формулу для центростремительного ускорения. Почему центростремительного? Да потому, что вектор a направлен к центру. В этом нетрудно убедиться, подсчитав скалярное произведение:

a · r	=	axx + ayy = –(ω ^2 r cos ω t) r cos ω t +
	+	(– ω ^2 r sin ω t) r sin ω t = – ω ^2 r ^2.	(11)

С другой стороны,

(12)

Из сравнения двух этих выражений получаем, что . Таким образом, вектор ускорения антипараллелен вектору r, то есть направлен к центру. В результате картина направлений векторов выглядит, как показано на рис. 2.

Рис. 2. Радиус-вектор, скорость и ускорение материальной точки при равномерном движении по окружности.

До сих пор при рассмотрении вращательного движения мы оперировали проекциями векторов на оси координат. Между тем, часто бывает полезно иметь соотношения, не зависящие от выбора системы координат, или, как говорят, записанные в векторной форме. Примером таких соотношений является выражение для координаты и скорости частицы при равноускоренном движении (см. лекцию 2).

При рассмотрении вращательного движения мы ввели угловую скорость вращения ω как производную по времени от угла поворота α: ω = dα / dt. Давайте теперь зададимся вопросом, какой величиной, скалярной или векторной, является угол поворота. Ведь когда говорят о повороте, нужно указывать не только величину угла поворота, но и то, вокруг какой оси происходит вращение (поворот) и в какую сторону (по часовой стрелке или против). В разобранном выше примере осью вращения была ось z и, поскольку мы использовали правую систему координат, вращение происходило по часовой стрелке (если смотреть в положительном направлении вдоль оси z) (pис. 3).

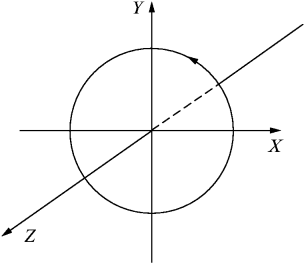Рис. 3. Направление вращения.

С этой точки зрения угол поворота должен быть величиной векторной. Однако, как мы убедимся на следующей лекции, произвольный угол поворота вектором, вообще говоpя, не является. Понятие вектора применимо лишь по отношению к бесконечно малым углам поворота.

Поэтому, говоря о повороте на какой-то малый угол Δα, можно приближенно говорить о векторе Δ α, величина которого равна углу поворота, а направление показывает направление оси вращения так, чтобы поворот происходил по часовой стрелке, или в соответствии с правилом буравчика. В нашем конкретном случае вектор Δ α коллинеарен с направлением оси z. Зададимся вопросом, как связано перемещение материальной точки Δ r при повороте ее радиус-вектора r на малый угол Δ α (pис. 4).

Рис. 4. Связь вектора перемещения с углом поворота.

На этот вопрос легко ответить, если речь идет о бесконечно малых поворотах d α. Тогда бесконечно малым является и перемещение d r. Его величина (равная длине хорды) совпадает теперь с длиной дуги, то есть

| dr | = rdα,

(13)

а по направлению вектор d r совпадает с касательной, то есть перпендикулярен r. В результате мы имеем три взаимно перпендикулярные вектора r, d r и d α, образующие правую тройку (pис. 5),

Рис. 5. Взаимная ориентация трех векторов.

причем | d r | = | d α | | r |. Те, кто помнят из школьного курса о векторном произведении векторов, без труда сообразят, что искомое соотношение можно записать в виде векторного равенства

dr = [ dα × r ].

(14)

Действительно, по определению, векторным произведением двух векторов [ A × B ] называется вектор

C = [ A × B ],

(15)

который направлен перпендикулярно плоскости, в которой лежат (или которую образуют) два вектора A и B, в сторону от этой плоскости, соответствующую правилу буравчика (см. рис. 6).

Рис. 6. Оpиентация тpех вектоpов в векторном произведении.

Величина же вектора C равна произведению модулей векторов на синус угла между ними:

(16)

В нашем случае угол между векторами d α и r равен 90^°, так что синус равен единице. А поскольку, как мы уже писали, | d r | = r dα, то мы убеждаемся в справедливости векторного соотношения d r = [ d α × r ].

Разделив обе стороны этого равенства на бесконечно малый временной интервал dt, в течение которого произошло изменение вектора r на d r, мы получим

(17)

Но величина, стоящая в левой части равенства, есть не что иное, как скорость частицы v, а производная

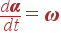
(18)

называется вектором угловой скорости. Ее мы вначале ввели по абсолютной величине, а теперь показали, что имеет смысл говорить об угловой скорости вращения как о векторе. Ее величина определяет величину угловой скорости (скорость вращения, или скорость изменения угла), а направление параллельно оси вращения, причем так, что имеет место правило буравчика. Итак, мы получили, что

v = [ ω × r ].

(19)

Оpиентация этих тpех вектоpов показана на pис. 7.

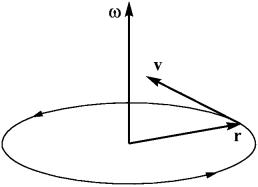Рис. 7. Ориентация радиус-вектора, вектора скорости и угловой скорости.

Чтобы получить ускорение a, надо от обеих частей взять производную по времени. Если ω постоянно (как по величине, так и по направлению) ¹ , то

(20)

то есть ускорение оказывается перпендикулярным угловой скорости вращения ω и скорости движения v. А поскольку последняя направлена по касательной, то, значит, ускорение направлено либо параллельно r, либо антипараллельно. Как именно, можно выяснить, подставив в вышеприведенную формулу значение v: ²

a	=	[ ω × v ] = [ ω × [ ω × r ]] =
	=	ω (ω · r)– r (ω · ω) = ω (ω · r)– ω ^2 r.	(21)

Поскольку в рассматриваемом нами примере начало кооpдинат выбpано в центpе окpужности, то угловая скорость ω и радиус-вектор r перпендикулярны друг другу а, следовательно, их скалярное произведение равно нулю (вообще говоря, как мы сейчас увидим, далеко не всегда 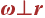) и мы получаем

a = – ω ^2 r,

(22)

то есть антипараллельность векторов a и r (вспомните термин «центростремительное ускорение»). По величине они таковы: | a | = ω ²| r |, то есть имеем уже знакомый результат.

Вы можете спросить, зачем нам понадобилось иметь дело с векторным и с двойным векторным произведением, если мы уже разобрали движение по окружности, дифференцируя по времени проекции материальной точки на оси координат (причем получили результаты, известные со школьной скамьи). Стоит ли игра свеч? Да, стоит, во-первых, потому, что мы записали законы движения в инвариантной, как говорят, форме, не зависящей от выбора конкретной системы координат. Во-вторых, записанные нами соотношения справедливы и в более общем случае, когда мы рассматриваем вращение системы материальных точек или твердого тела как целого (pис. 8).

Рис. 8. Вращение твердого тела.

Имея в виду эту картину, нетрудно показать, что здесь, хотя ω и r не перпендикулярны друг другу, тем не менее, выполняется прежнее соотношение для скорости движения некоторой выбранной нами точки с радиус-вектором r:

v = [ ω × r ].

(23)

Действительно, как следует из рис. 8, точка движется по окружности радиуса ρ = r sin β со скоростью υ = ωρ = ω r sin β. Но поскольку β — это угол между векторами ω и r, мы убеждаемся в справедливости этой формулы.

Теперь нам понятно происхождение дополнительного слагаемого в центростремительном ускорении (см. pис. 9):

a = ω (ω · r)– ω ^2 r.

(24)

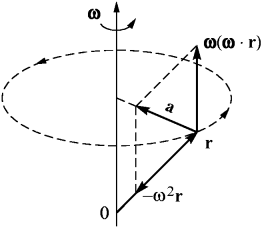Рис. 9. Центростремительное ускорение.

Таким образом, ускорение a на самом деле направлено не к центру, а к оси вpащения, поэтому его можно было бы называть осестремительным. Но, pазумеется, дело не в названиях.

В пользу соотношения v = [ ω × r ] говорит и то, что оно справедливо в более общем случае, когда вектор угловой скорости ω не является постоянным и зависит от времени: ω (t). Тогда формула для ускорения изменится — в ней появится дополнительное слагаемое:

a	=
	=	[ β × r ]+ [ ω × v ].	(25)

Величина β = d ω / dt называется угловым ускорением. Оно появляется, если меняется по величине угловая скорость (замедляется, например, вращение вокруг фиксированной оси) либо поворачивается с течением времени сама ось вращения (либо и то и другое).

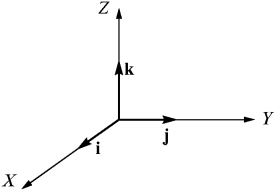Рис. 10. Взаимное расположение единичных ортов.

В заключение для справок приведем выражение для декартовых компонент векторного призведения C = [ A × B ]:

Cx	=
Cy	=		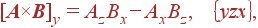(26)
Cz	=

Здесь для запоминания следует использовать указанные выше циклические перестановки. Эти соотношения легко доказываются, если записать каждый вектор в виде

A = Axi + Ayj + Azk

(27)

и, аналогично, вектор B. Затем следует учесть, что векторные призведения единичных ортов i, j и k между собой равны соответственно (см. pис. 10)

[ i × j ] = k, [ k × i ] = j, [ j × k ] = i

(28)

и что при изменении порядка сомножителей изменяется знак векторного произведения:

[ j × i ] = – [ i × j ] и т. д.

(29)

Далее нужно произвести векторное умножение

(30)

воспользовавшись приведенными выше правилами.

¹Равномерное вращение.

²Здесь мы воспользовались формулой для двойного векторного произведения [ A × [ B × C ] = B (A · C)– C (A · B).

Литература:

1.Архангельский М.А.

Курс физики. Механика.

2.Савельев

Курс общей физики. Том1.

3Домашний репетитор по физике.

Дата добавления: 2014-01-06