Лекция №7 Движение тела переменной массы. Уравнение Мещерского и Циолковского

Лекция № 6 Система материальных точек. Силы внешние и внутренние. Движение системы материальных точек. Центр масс и центр тяжести механической системы. Движение центра масс. Замкнутые системы. Закон сохранения импульса замкнутой механической системы. Постоянство скорости центра масс и замкнутой системы.

Заключение

Итак, длительность события (времени), размеры тела не являются абсолютными величинами, а зависят от скорости тела, т. е. являются относительными. Кроме того масса и энергия оказались связанными друг с другом, хотя они являются качественно различными свойствами материи. Основной вывод теории относительности сводится к тому, что пространство и время взаимосвязаны и образуют единую форму существования материи: пространство-время. Наиболее общая теория пространства-времени называется общей теорией относительности или теорией тяготения, т.к. согласно этой теории свойства пространства-времени в данной области определяются действующими в ней полями тяготения

.В изложенной выше теории действием тяготения Эйнштейн пренебрег. Поэтому она называется частной (или специальной) теорией относительности т. к. она является частным случаем общей теории относительности, завершенной Эйнштейном позже, в 1915 г.

До сих пор мы изучали взаимодействие двух тел и часто, рас­сматривая движение одного тела, заменяли другое, с которым пер­вое взаимодействует, соответствующей силой. Но изучение законов движения одного или двух тел не исчерпывает всех возможных за­дач о механическом движении, с которыми мы сталкиваемся при изучении природы или в технике. Нередко приходится иметь дело с движением совокупности взаимодействующих между собой тел, или с движением, как говорят, механической системы. Пример механических систем; любая машина, тепловоз с вагонами, Солнце и планеты, ракетный поезд и т. п., а также любое тело, если в дан­ной задаче его приходится рассматривать как совокупность частиц.

Если движение таково, что размеры и форма отдельных тел, образующих систему, не играют роли, то рассматривается задача о движении системы материальных точек.

Силы, действующие между телами системы, называются внут­ренними для данной системы силами.

Силы, действующие на тела системы со стороны тел, не входя­щих в данную систему, называются внешними силами.

Одна и та же сила в зависимости от постановки задачи может быть внутренней или внешней. Например, силы взаимного притя­жения планет и Солнца — внутренние силы, если мы рассматриваем солнечную систему как целое, и внешние по отношению к каждой отдельно взятой планете, когда, скажем, мы решаем задачу о дви­жении Земли и Луны, о приливных явлениях на поверхности Земли и т. п.

Под воздействием сил каждая из материальных точек системы, вообще говоря, как-то изменяет состояние своего движения, пере­мещаясь относительно других точек. Чтобы исследовать движе­ние системы в целом, надо, очевидно, исследовать движение каждой ее точки. Мы могли бы воспользоваться для этого законами Нью­тона, составить уравнения движения каждой точки системы и решить их. Но такой путь решения задачи о движении системы часто оказывается весьма сложным либо вследствие того, что трудно

определить внутренние силы в виде известной функции (например, при быстро протекающих взаимодействиях тел типа удара), либо потому, что исследуемая система состоит из очень большого числа материальных точек (например, при исследовании движения не­которого объема жидкости). Однако в ряде слизвестной функции (например, при быстро протекающих взаимодействиях тел типа удара), либо потому, что исследуемая система состоит из очень большого числа материальных точек (например, при исследовании движения не­которого объема жидкости). Однако в ряде случаев более общее понятие, не зависящее от силы тяжести,— центр масс системы. Центром масс двух материальных точек называется точка, делящая расстояние между ними в отношении, обратно пропорциональном их массам (рис. 1).

Пусть имеем две материальные точки массой m1 и m2, коорди­наты которых в неподвижной системе отсчета соответственно x1, y1, z1 и x2, y2, z2. По известному правилу аналитической геометрии координаты точки x, y, z, делящей отрезок в заданном отношении 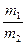, связаны с координатами концов отрезка следующим соотношением: 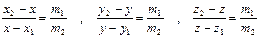(1)

Решая эти равенства относительно x, y, z, получим:

(2)

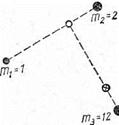Центром масс трех материальных точек называет­ся точка, которая делит расстояние между центром масс двух из них и третьей точкой в отношении, обратно пропорциональном сумме масс двух первых точек и мас­се третьей из них (рис. 1).

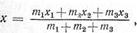
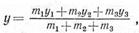Легко получить координаты центра масс трех материальных точек, подобно тому как это сделано выше для двух точек:

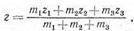Рис.1

Прибавляя к системе четвертую, пятую и т. д. точки, получим, что координаты центра масс системы n материальных точек:

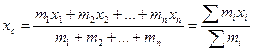(4)

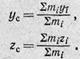
Рассмотрим действие друг на друга двух изолированных тел не взаимодействующих с другими телами. Будем считать силы во все время взаимодействия постоянными. В соответствии со вторым законом динамики изменение количества движения первого тела Δ(mυ)₁ равно импульсу силы F₁₂, действующей на него со стороны второго тела:

(5)

где Δt — интервал времени взаимодействия.

Изменение количества движения второго тела:

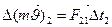(6)

где F₁₂ — сила, действующая со стороны первого тела на второе. Согласно третьему закону Ньютона

и, кроме того, очевидно,

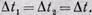
Следовательно,

(7) или

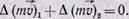(8)

Независимо от природы сил взаимодействия и дли­тельности их действия общее количество движения двух изолированных тел остается постоянным.

Полученный результат может быть распространен на любое чис­ло взаимодействующих тел и на силы, меняющиеся со временем. Для этого интервал времени Δt, в течение которого происходит взаимодействие тел, разобьем на столь малые промежутки dt, в

течение каждого из которых силу можно с заданной степенью точности считать постоянной. В течение каждого промежутка вре­мени будет выполняться соотношение (8). Следовательно, оно будет справедливо и для всего интервала времени Δt.

Для обобщения вывода на n взаимодействующих тел введем по­нятие замкнутой системы.

Замкнутой называется система тел, для которой результирую­щая внешних сил равна нулю.

Пусть n материальных точек массами m₁, m₂,…, m_n образуют замкнутую систему. Изменение количества движения каждой из этих точек в результате взаимодействия ее со всеми остальными точками системы соответственно:

...; .

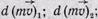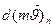Обозначим внутренние силы, действующие на точку массой m₁ со стороны других точек, через F₁₂, F₁₃,..., F_1n, на точку массой m₂ — F₂₁, F₂₃,..., F_2n и т. д. (Первый индекс обозначает точку, на которую действует сила; второй индекс указывает точку, со стороны которой действует сила.)

Запишем в принятых обозначениях второй закон динамики для каждой точки в отдельности: 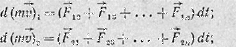(9)

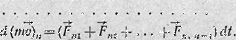
Число уравнений равно числу n тел системы. Чтобы найти общее изменение количества движения системы, нужно подсчитать геоме­трическую сумму изменений количества движения всех точек систе­мы. Просуммировав равенства (9), мы получим в левой части пол­ный вектор изменения количества движения системы за время dt, а в правой части — элементарный импульс результирующей всех сил, действующих в системе. Но так как система замкнута, то ре­зультирующая сил равна нулю. В самом деле, по третьему закону динамики каждой силе F_ik в равенствах (9) соответствует сила F_ki причем

F_ik = — F_ki т. е.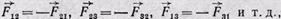

и результирующая этих сил равна нулю. Следовательно, во всей замкнутой системе изменение количества движения равно нулю:

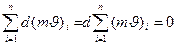(10)

или

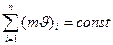(11)

Полное количество движения замкнутой системы — величина постоянная во все время движения (закон сохра­нения количества движения).

Закон сохранения количества движения — один из фундамен­тальных законов физики, справедливый как для систем макроско­пических тел, так и для систем, образованных микроскопическими телами: молекулами, атомами и т. п.

Если на точки системы действуют внешние силы, то количество движения, которым обладает система, изменяется.

Напишем уравнения (9), включив в них результирующие

внешних сил 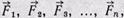действующих соответственно на

первую, вторую и т. д. до n-й точки:

(12)

Сложив левые и правые части уравнений, мы получим: слева — полный вектор изменения количества движения системы; справа — импульс результирующей внешних сил:

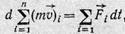
или, обозначая результирующую внешних сил F:

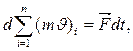(13)

т. е.изменение полного количества движения системы тел равно импульсу результирующей внешних сил.

Равенство (13) может быть записано в другом виде:

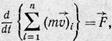(14)

т. е. производная по времени от общего количества движения системы точек равна результирующей внешних сил, дей­ствующих на точки системы.

Рис. 2.

Проецируя векторы количества движения системы и внешних сил на три взаимно перпендикулярные оси, вместо векторного ра­венства (14) получим три скалярных уравнения вида:

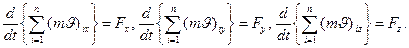(15)

Если вдоль какой-либо оси, скажем OY, составляющая резуль­тирующей внешних сил равна нулю, то количество движения вдоль этой оси не изменяется, т. е., будучи вообще незамкнутой, в направ­лении 0Y система может рассматриваться как замкнутая.

Мы рассмотрели передачу механического движения от одних тел к другим без перехода его в другие формы движения материи. Величина «mυ оказывается здесь мерой просто перенесенного, т. е. продолжающегося, движения...».

Применение закона изменения количества движения к задаче о движении системы тел позволяет исключить из рассмотрения все внутренние силы, что упрощает теоретические исследования и ре­шения практических задач.

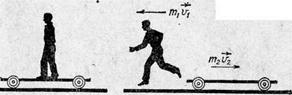
1. Пусть на покоящейся тележке неподвижно стоит человек (рис. 2). Количество движения системы человек — тележка рав­но нулю. Замкнута ли эта система? На нее действуют внешние силы — сила тяжести и сила трения между колесами тележки и полом. Вообще говоря, система не замкнута. Однако, поставив тележку на рельсы и соответствующим образом обработав поверх­ность рельсов и колес, т. е. значительно уменьшив трение между ними, можно силой трения пренебречь.

Сила тяжести, направленная вертикально вниз, уравновеши­вается реакцией деформированных рельсов, и результирующая этих сил не может сообщить системе горизонтального ускорения, т. е. не может изменить скорость, а следовательно, и количество дви­жения системы. Таким образом, мы можем с известной степенью приближения считать данную систему замкнутой.

Положим теперь, что человек сходит с тележки влево (рис. 2), имея скорость υ₁. Чтобы приобрести эту скорость, человек должен, сократив свои мышцы, подействовать ступнями ног на площадку тележки и деформировать ее. Сила, действующая со стороны деформированной площадки на ступни человека, сообщает телу человека ускорение влево, а сила, действующая со стороны деформированных ступней человека (в соответствии с третьим законом динамики), сооб­щает тележке ускорение вправо. В результате, когда взаимодейст­вие прекратится (человек сойдет с тележки), тележка приобретет не­которую скорость υ₂.

Для нахождения скоростей υ₁ и υ₂ с помощью основных законов динамики надо было бы знать, как меняются силы взаимодействия человека и тележки со временем и где приложены эти силы. Закон сохранения количества движения позволяет сразу найти отношение скоростей человека и тележки, а также указать их взаимную на­правленность, если известны значения масс человека m₁ и тележ­ки m₂.

Пока человек неподвижно стоит на тележке, общее количество движения системы равно нулю. С точностью, позволяющей пре­небречь действием внешней силы трения, после того как человек сходит с тележки со скоростью υ₁ количество движения системы остается равным нулю: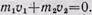

Отсюда

или

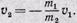
Скорости, приобретенные человеком и тележкой, обратно про­порциональны их массам. Знак «минус» указывает на их противопо­ложную направленность.

2. Если человек, двигаясь со скоростью υ₁ вбегает на неподвиж­но стоящую тележку и останавливается на ней, то тележка прихо­дит в движение, так что общее количество движения ее и человека оказывается равным количеству движения, которым обладал рань­ше человек один: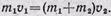

3. Человек, движущийся со скоростью υ₁ вбегает на тележку, перемещающуюся ему навстречу со скоростью υ₂, и останавливается на ней. Далее система человек — тележка движется с общей скоростью υ. Общее количество движения человека и тележки равно сумме количеств движения, которыми они обладали каждый в от­дельности:

4. Использовав то обстоятельство, что тележка может переме­щаться только вдоль рельсов, можно продемонстрировать вектор­ный характер изменения количества движения. Если человек вхо­дит и осколичеств движения, которыми они обладали каждый в от­дельности:

4. Использовав то обстоятельство, что тележка может переме­щаться только вдоль рельсов, можно продемонстрировать вектор­ный характер изменения количества движения. Если человек вхо­дит и осе, чем в первом (cos 45°~0,7), а в третьем случае те­лежка неподвижна (cos 90°=0).

Покажем,что поступательное движение механической системы как целого можно характеризовать движением одной точки- центра масс системы, считая, что в ней сосредоточена масса всех тел, входящих в систему.

Перепишем равенства(4) в виде

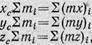(16)

продифференцируем по времени:

(17)

В равенствах (17) слева стоит произведение суммарной массы тел 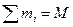,образующих систему, а справа — компоненты вектора пол­ного количества движения тел системы:

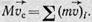(18)

Полное количество движения механической системы равно количеству движения материальной точки мас­сой, равной массе тел системы и движущейся, как дви­жется ее центр масс.

Продифференцируем равенство (18) по времени и сравним с выражением (14). В равенстве (18) после дифференцирования справа, а в равенстве (614) слева стоит одна и та же величина — производная от вектора полного количества движения тел системы. Следовательно,

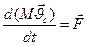(19)

где (M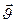) — количество движения центра масс системы, F — век­тор результирующей внешних сил, действующих на тела системы. Центр масс механической системы движется так же, как двигалась бы материальная точка, в которой сосредоточена масса всех тел системы, под действием результирующей внешних сил, приложенных к телам, образующим систему.

Если механическая система замкнута, т. е. F=0, то

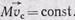
Центр масс замкнутой механической системы нахо­дится в покое или движется равномерно и прямолинейно.

Закон движения центра масс механической системы не дает пол­ной картины движения отдельных ее тел, но позволяет установить некоторые важные особенности движения системы в целом.

Рассмотрим, например, движение солнечной системы. С боль­шой степенью точности ее можно считать замкнутой, пренебрегая взаимодействием с другими космическими телами. Следовательно, центр масс солнечной системы можно считать движущимся прямоли­нейно и равномерно.

Рассмотрим твердое тело, находящееся в покое. Положим, на него одновременно подействовали двумя силами, равными по величине, но противоположно направленными и приложенными в двух точках А иВ, не совпадающих с центром масс (рис. 3). Такая система сил называется парой сил. Каков характер движения тела?

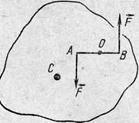
Рис. 3. Тело под действи­ем пары сил поворачивает­ся вокруг центра масс.

Результирующая приложенных к телу внешних сил равна нулю. Следовательно, центр масс тела должен остаться в покое. Тело, одна точка которого неподвижна, может, очевидно, только вращаться вокруг этой точки. И, следовательно, тело под действием приложенной пары сил будет поворачиваться вокруг центра масс С. Иногда, руководствуясь только интуицией, приходят к ошибочному заключению, что в описанном случае тело должно вращать­ся вокруг точки О, расположенной между точками приложения пары сил.

В природе и современной технике мы нередко сталкиваемся с движением тел, масса которых меняется со временем. Масса Земли возрастает вследствие падения на нее метеоритов, масса метеорита при полете в атмосфере уменьшается в результате отрыва или сго­рания его частиц, масса дрейфующей льдины возрастает при намер­зании и убывает при таянии и т. д. Движение якоря с якорной цепью, когда все большее число звеньев цепи сходит с лебедки,— пример движения тела переменной массы. Ракеты всех систем, реактивные самолеты, реактивные снаряды и мины также являются телами, масса которых изменяется во время движения.

Общие законы динамики тел с переменной массой были открыты и исследованы И. В. Мещерским и К. Э. Циолковским. Циолков­ским были разработаны фундаментальные проблемы реактивной техники, которые в наши дни служат основой для штурма человеком межпланетных пространств.

Для вывода основного уравнения движения тела переменной массы рассмотрим конкретный случай движения простейшей ра­кеты (рис. 4).

Мы будем рассматривать ракету как достаточно малое тело, положение центра тяжести которого не меняется по мере сгорания пороха. В этом случае мы можем считать ракету материальной точ­кой переменной массы, совпадающей с центром тяжести ракеты.

Не рассматривая физико-химическую природу сил, возникаю­щих при отбрасывании от ракеты газов, образованных при сго­рании пороха, сделаем такое упрощающее вывод предположение: будем считать, что отбрасываемая от ракеты частица газа dM взаимодействует с ракетой М только в момент их непосредственного контакта. Как только частица dM приобретает скорость относитель­но точки М, ее воздействие на нее прекращается. Предположим далее, что изменение массы ракеты М происходит непрерывно, без скачков. (Это значит, что мы не рассматриваем многоступен­чатые ракеты, масса которых меняется скачкообразно.) Это пред­положение позволяет считать, что существует производная от мас­сы по времени.

Пусть в момент t масса ракеты М, а ее скорость относительно неподвижной системы координат(рис. 5). Положим, за время dt от ракеты отделилась частица массы (—dM) со скоростью (относи­тельно той же неподвижной системы координат), равной и. Знак «минус» перед приращением массы указывает на то, что приращений это отрицательное, масса ракеты убывает.

Положим, равнодействующая внешних сил, действующих на ракету (силы тяжести и сопротивления среды), F. Как сказано выше, в момент отделения частицы массы (—dM) между ней и ра­кетой действует неизвестная нам реактивная сила Fp. Сила Fp для системы ракета — частица является внутренней. Чтобы исключить

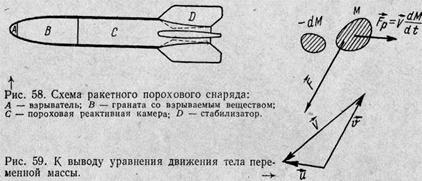
ее из рассмотрения, воспользуемся законом изменения количества движения. Количество движения системы ракета — частица в момент t, т. е. перед отделением частицы:

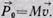
Количество движения системы в момент t+dt (после отделения частицы) складывается из количества движения массы [М—(—dM)], получившей скорость (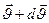), и количества движения массы частицы — dM, летящей со скоростью :

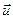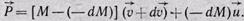(20)

Изменение количества движения системы за время dt:

Величина dP должна быть приравнена импульсу равнодействующей внешних сил

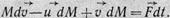(21)

Отсюда, перегруппировав члены и разделив на dt, получим ос­новное уравнение движения точки переменной массы:

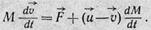(22)

Это уравнение иначе называют уравнением Мещерского. Для ракеты <0, так как при полете масса ее убывает. Если масса тела во время движения увеличивается, то > 0. При =0 уравнение (22) переходит в уравнение второго закона Нью­тона для случая постоянной массы.. Величина u — 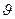есть скорость выбрасываемых ракетой частиц относительно системы координат, движущейся с ракетой. Эту скорость называют обычно просто относительной скоростью V. Тогда равенство (22) запишется в виде

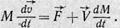(23)

Для любого момента времени произведение массы те­ла на его ускорение равно векторной сумме равнодействующей приложенных к телу внешних сил и реак­тивной силы. При движении ракеты вблизи Земли равнодействую­щая внешних сил представляет собой сумму силы тяжести и силы сопротивления воздуха. Ускорение ракеты зависит еще и от реактивной силы, изменяя величину и направление которой мож­но управлять полетом ракеты.

Если относительная скорость отбрасываемых частиц равна 0, то следует

M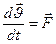

Важный вклад в механику тел переменной массы применительно к конкретным задачам реактивной техники внесен знаменитым рус­ским ученым Константином Эдуардовичем Циолковским. В 1903 г. была издана его работа «Исследование мировых пространств ре­активными приборами», в которой К. Э. Циолковский исследовал ряд случаев прямолинейных движений ракет. К. Э. Циолковским обоснована и доказана возможность практического использования реактивного движения. Им найдены условия, при которых можно получить скорости, достаточные для осуществления космического полета. Полученная им формула, связывающая скорость ракеты с ее начальной массой, до сих пор используется для предваритель­ных расчетов. В работах 1911—1914 гг. он изучил вопрос о вели­чине запасов топлива, необходимых для преодоления сил тяготения Земли, и предложил высококалорийное топливо, позволяющее получить большие скорости истечения газовых струй. К. Э. Циол­ковского по праву считают изобретателем жидкостных ракет даль­него действия и основоположником теории межпланетных полетов.

Ему принадлежит идея разработки теории так называемых многоступенчатых ракет, когда на некоторых интервалах времени масса ракеты меняется непрерывно, а в некоторые моменты — скачком.

Им проведены большие исследования по оценке сил сопро­тивления при движении тел переменной массы. К. Э. Циолковским поставлен целый ряд оригинальных проблем, имеющих решающее значение для развития реактивной техники.

Для того чтобы выяснить основные факторы, создающие воз­можность реактивного движения с большими скоростями, рас­смотрим движение точки переменной массы в безвоздушном про­странстве (отсутствует сопротивление движению тела), без действия внешних сил (силы тяготения). Предположим, что скорость исте­чения частиц направлена прямо противоположно вектору скорости

тела 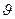. Эти условия соответствуют так называемой первой задаче Циолковского. В результате получаем формулу Циолковского и следствие из нее. Найдем при сделанных предположениях скорость движения тела (точки) и закон ее движения.

При сформулированных условиях уравнение движения приобре­тает вид:

M (25) или

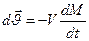(26)

Положим, M=Mof(t), где f(t)— функция, определяющая закон изменения массы.)=1. Подставив в (26) значение М и проинтегрировав, получим:

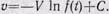
Для определения постоянной С учтем, что при t==0 f(0)=1 и 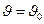, тогда C=и

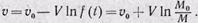(27)

Эта формула носит название формулы Циолковского. Из формулы следует, что скорость, приобретенная точкой переменной массы, зависит от относительной скорости V и отношения начальной массы к остающейся к концу процесса горения. Если масса точки в конце процесса горения M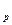, а отброшенная масса (масса топлива)— m, то при нулевой начальной скорости получаем для расчета скорости в конце процесса горения выражение:

Отношение 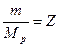называют числом Циолковского. Для современ­ных ракет можно положить V=2000 м/сек. Тогда при числе Циол­ковского Z=0,250; 9,000; 32,333; 999,000 получим соответственно cкорости 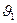=446; 4605; 7013; 13 815 м/сек. Из формулы Циолковcкого (27) следует, что:

1) скорость точки переменной массы в конце активного участка тем больше, чем больше скорость отбрасывания частиц;

2) скорость в конце активного участка тем больше, чем больше скорость отбрасывания частиц число Циолковского;

3)скорость точки переменной массы в конце активного участка не зависит от закона изменения массы (режима горения). Задан­ному числу Циолковского соответствует определенная скорость точки в конце процесса горения независимо от того, быстро или
медленно шло горение. Это следствие является проявлением за­кона сохранения количества движения;

4)для получения возможно больших скоростей точки перемен­ной массы в конце активного участка выгоднее идти по пути уве­личения относительной скорости отбрасывания частиц, чем по пути увеличения запасов топлива.

Из уравнения (27) можно найти закон изменения расстояния излучающей точки от начала координат; полагая V=const, полчим:

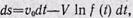(28)

после интегрирования:

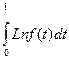s=s+t-V (29)

Отсюда следует, что закон расстояния в отличие от закона скорости зависит от закона изменения массы, т. е. от функции f(t).

Дата добавления: 2014-01-06