Лекция11

.

Пара сил. Момент пары. Закон сохранения момента импульса твердого тела и примеры его проявления. Вычисление моментов инерции тел. Теоремы Штейнера-Гюйгенса. Кинетическая энергия вращательного движения.

Пара сил — это две равные по величине и противоположные по направлению параллельные силы, приложенные к одному телу. Пара сил не имеет равнодействующей. Кратчайшее расстояние между линиями действия сил, образующих пару сил, называют плечом пары. Действие пары сил на тело характеризуется моментом пары сил — произведением одной из сил на плечо.

Найдем значение вектора момента пары сил.

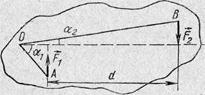
Положим, к телу приложена пара сил и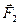. Рассечем тело плоскостью, в которой лежат силы (рис. 3).

рис. № 3. Момент пары сил.

Возьмем произволь­ную точку О, лежащую в этой плоскости. Момент силы относи­тельно этой точки M₁=F₁OA 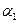и направлен перпендикулярно плоскости чертежа к нам. Момент силы равен M₂=F₂OB и направлен перпендикулярно плоскости чертежа от нас Суммарный момент пары сил равен алгебраической сумме моментов M_t и М₂:

M=.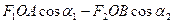

Но поскольку ,

.

Выражение, стоящее в скобках, представляет собой расстояние между линиями действия сил. Обозначим это расстояние через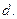

Тогда

,

где d — плечо пары сил.

Вектор момента пары сил численно равен произве­дению величины одной из сил пары на плечо пары. Он направлен в сторону поступательного движения бу­равчика, рукоятка которого вращается по направле­нию сил пары.

В механике имеется три закона сохранения: импульса, энергии и момента импульса. Все они являются следствиями законов движения. Ограничимся лишь простыми частными случаями.

Если при вращении тела вокруг неподвижной оси момент внешних сил относительно этой оси равен нулю, то равна нулю производная момента импульса тела:

Это означает, что сам момент импульса остается постоянным:

Из неизменности момента инерции J твердого тела, вращающегося вокруг определённой оси, следует постоянство угловой скорости вращения. Так, если бы не было трения, то не менялась бы угловая скорость вращающегося на оси колеса.

Последнее уравнение и является формой закона сохранения момента импульса для частного случая вращения вокруг неподвижной оси. В общем случае этот закон формулируется так: в замкнутой системе тел полный (суммарный) момент импульса остаётся постоянным.

Если момент внешней силы, действующей на тело, равен нулю, то уравнение выполняется и в том случае, когда тело не является твёрдым, т.е. когда момент его инерции может изменяться. Причём в этом случае закон сохранения момента импульса позволяет простым путём получить важные заключения о характере вращения тела.

Все вы могли видеть, как балерина или конькобежец-фигурист легко меняет скорость своего вращения, не отталкиваясь от пола или льда. То же явление можно наблюдать и по-другому. Человек становится на круглую платформу, которая может вращаться вокруг вертикальной оси без заметного трения (скамья Жуковского). Оттолкнувшись затем от пола, он начинает вращаться, Меняя затем положение рук (лучше с тяжёлыми предметами в ладонях), т.е. меняя момент инерции тела, человек тем самым меняет и угловую скорость вращения,

Для вычисления момента инерции необходимо мысленно рас­членить тело на достаточно малые элементы, точки которых можно считать лежащими на одинаковом расстоянии от оси вращения, затем найти произведение массы каждого элемента на квадрат его расстояния от оси и, наконец, просуммировать все полученные про­изведения. Очевидно, это весьма трудоемкая задача. Для подсчета моментов инерции тел правильной геометрической формы можно воспользоваться в ряде случаев приемами интегрального исчисле­ния.

Нахождение конечной суммы моментов инерции элементов тела заменим суммированием бесконечно большого числа моментов инер­ции, вычисленных для бесконечно малых элементов:

Вычислим в качестве примера момент инерции однородного диска или сплошного цилиндра высотой h относительно его оси симметрии (рис. 4).

рис.№4 Вычисление момента инерции однородного диска

Расчленим диск на элементы в виде тонких концентрических колец с центрами на оси его симметрии. Полученные кольца имеют внутренний диаметр r и внешний r-dr, а высоту h. Так как dr<<r, то можем считать, что расстояние всех точек кольца от оси равно r. Для каждого отдельно взятого кольца момент инерции 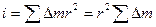где, — масса всего кольца. Объем кольца . Если плотность мате­риала диска 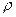, то масса кольца .

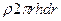Момент инерции кольца . Чтобы подсчитать момент инерции всего диска, надо просуммировать моменты инерции колец от центра диска () до края его (r=R),

т. е. вычислить интеграл:

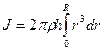
или

Но масса диска 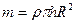, следовательно,

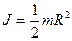
Приведем (без вычисления) моменты инерции для некоторых тел правильной

геометрической формы, выполненных из однород­ных материалов (рис. 5).

1. Момент инерции тонкого кольца относительно оси, проходя­щей через его центр перпендикулярно его плоскости (или тонко­стенного полого цилиндра относительно его оси симметрии):

2. Момент инерции толстостенного цилиндра относительно оси симметрии:

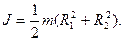
где 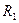— внутренний и R₂ — внешний радиусы.

3. Момент инерции диска относительно оси, совпадающей с од­ним из его диаметров:

4. Момент инерции сплошного цилиндра относительно оси, пер­пендикулярной образующей и проходящей через ее середину:

,

где R — радиус основания цилиндра, h — высота цилиндра

5. Момент инерции тонкого стержня относительно оси, прохо­дящей через его середину:

,

где — длина стержня.

6 Момент инерции тонкого стержня относительно оси, прохо­дящей через один из его концов:

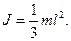
7. Момент инерции шара относительно оси, совпадающей содним из его диаметров:

рис.№5 К расчёту моментов инерции различных тел:

1—кольца относительно оси, проходящей через центр перпендикулярно его плоскости; 2 — полого цилиндра относительно оси симметрии, параллельной образующим; 3 — тонкого диска относительно оси, совпадающей с диаметром; 4 — сплошного цилиндра относитель­но оси симметрии, перпендикулярной образующим; 5 — однородного стержня относитель­но оси, проходящей через середину перпендикулярно к нему; 6 — однородного стержня от­носительно оси, проходящей через конец стержня; 7 — шара относительно оси, совпадаю­щей с диаметром.

Если известен момент инерции какого-либо тела относительно оси, проходящей через его центр масс, то момент инерции относи­тельно любой другой оси, параллельной первой, может быть найден на основании так называемой теоремы Гюйгенса:

Момент инерции тела J относительно любой оси равен моменту инерции тела 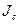относительно оси, параллельной данной и проходящей через центр масс тела, плюс масса тела т, умноженная на квадрат расстояния между осями:

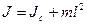
Кинетических энергия твердого тела конечных размеров равна сумме кинетических энергий элементов, на которые расчленено тело. В общем случае тело может двигаться поступательно и однов­ременно вращаться. Рассмотрим частный случай вращения тела

вокруг неподвижной оси.

Кинетическая энергия каждого элемента тела:

(**)

де m_i —масса 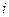-го элемента тела, 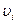— его линейная скорость.

Если расстояние центра элемента от оси вращения 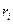то, при­нимая во внимание, что 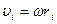, равенство (**) перепишем в виде:

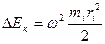
и, просуммировав по всем элементам, получим:

Но так как — момент инер­ции тела относительно выбранной оси, то

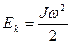
Эта формула отличается от соответствующей формулы для поступательного движения тем, что вместо линейной скорости в ней стоит угловая скорость, а вместо массы — момент инерции.

Рассмотрим изменение кинетической энергии вращающегося тела под действием сил. Положим, тело вращается вокруг непод­вижной оси 00. Пусть результирующая сила F, приложенная в точке А тела, отстоящей от оси на расстоянии r, лежит в плоскости траектории точки и направлена по касательной к ней (рис. 6).

рис.№6 К расчету работы при вращательном движении.

При повороте тела на угол точка приложения силы переме­стится на длину дуги 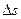. Если угол достаточно мал, то дугу ds мож­но считать равной перемещению ds. Тогда

элементарная работа силы F на пути ds:

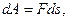
но

,

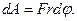
Так как

то

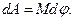
Полная работа при повороте на угол :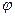

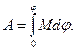
Если момент равнодействующей всех сил — величина постоянная, то из последнего соотношения получим:

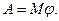
При вращательном движении работа измеряется про­изведением момента силы на угол поворота тела.

Если момент силы меняется со временем, то работа измеряется интегралом от момента силы по углу поворота.

Напишем основное уравнение динамики вращательного движе­ния:

Для подсчета работы умножим обе части равенства на угол поворота 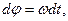где 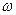—угловая скорость вращения и dt— весьма малый интервал времени, в пределах которого можно считать М=const:

Проинтегрировав левую и правую части последнего равенства, получи:

Т.е. изменение кинетической энергии тела при вращательном движении равно работе сил, момент которых сообщает телу угловое ускорение.

Полная кинетическая энергия твердого тела равна сумме кинетической энергии поступательного движения центра масс тела и кинетической энергии вращения тела:

,

где — скорость поступательного движения центра масс, J— момент инерции тела относительно оси вращения, проходящей через центр масс, 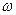—угловая скорость вращения тела вокруг своей оси.

Дата добавления: 2014-01-06