Законы Кеплера

Законы движения небесных тел, в частности движения планет вокруг Солнца, являются простым следствием основных законов механики, которые называют законами Ньютона, — трех законов динамики и закона всемирного тяготения.

Еще до Ньютона Кеплер на основе наблюдений Тихо Браге нашел законы движения планет вокруг Солнца. Эти законы носят название законов Кеплера и гласят следующее:

1. Орбиты всех планет являются эллипсами, в одном из фокусов которых находится Солнце.

2. Движение каждой планеты происходит так, что радиус-вектор, проведенный из центра Солнца к планете, за равные про­межутки времени «ометает» равные площади (рис.1).

3. Квадраты периодов обращения различных планет вокруг Солнца от­носятся, как кубы больших полуосей эллипсов орбит.

Рис.1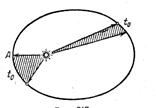

Первый закон Кеплера, следует из решения задачи об опре­делении орбит планет и закона движения их по орбите. Для этого вы­числяют траектории движения материальной точки, находящейся под действием центральной силы ), величина которой обратно пропор­циональна квадрату расстояния от центра. Результаты решения этой задачи показывают, что траектории небесных тел лежат в пло­скости и представляют собой или эллипс, или параболу, или гиперболу.

В частном случае, когда орбита планеты — окружность, элемен­тарным путем доказывается возможность такого движения под дей­ствием центральной силы. В самом деле, планета может двигаться по кругу тогда, когда сила притяжения ее Солнцем равна центро­стремительной силе. Чтобы планета из данного места, находяще­гося на расстоянии R от Солнца, могла двигаться по кругу, она должна иметь определенную скорость, направленную перпенди­кулярно к радиусу-вектору и равную)

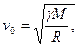(1)

где М — масса Солнца, а 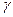— постоянная тяготения. Таким обра­зом, скорость движения по орбите и радиус орбиты связаны друг с другом, причем эта скорость не зависит от массы планеты.

Рис.2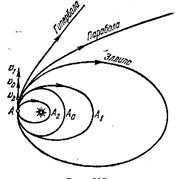

Более сложные вычисления показывают и наблюдения под­тверждают, что форма и вид орбиты связаны с начальной скоростью. Например, если скорость движения v₂ в точке А (рис.2) меньше v₀ из формулы (1), то планета будет двигаться по эллипсу так, что Солнце будет находиться в дальнем фокусе эллиптической орбиты (орбита АА₂ на рис.2). Если же скорость 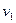больше «круговой», то планета также будет двигаться по эллипсу, но Солнце будет находиться в ближайшем фокусе орбиты (орбита АА_г на рис.2). Но движение по эллипсу происходит только в том случае, если ско­рость в точке А меньше скорости, равной

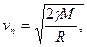(2)

при которой планета движется по параболе. Если же скорость движения в точке А больше «параболической» (см. формулу (2)), то небесное тело, которое в данном случае уже не может называться планетой, будет двигаться по ги­перболе и никогда не возвратится в ту же точку.

При движении по орбите остается постоянной сумма кинетической и потен­циальной энергий. Например, во время движения по эллипсу потенциальная энергия возрастает с увеличением расстоя­ния от Солнца, а кинетическая энергия соответственно падает, так что скорость в удаленных точках меньше, чем в ближай­ших к Солнцу. Если начальная скорость в точке А возрастает сверх «круговой» (1), то эллипс орбиты все увеличи­вается и вытягивается. Точка орбиты А₁ противоположная А₂, будет все удаляться от Солнца. Если мы знаем расстояние от Солнца в точке А₁, то по закону сохранения энергии можем определить скорость в этой точке в зависимости от начальной скорости в точке А. В самом деле, энергия в точке А

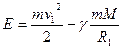(3)

равна энергии в любой точке траектории

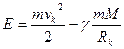(4)

где v_к и R_K — скорость в какой-то точке и ее расстояние от Солнца соответственно. Сравнивая формулы (3) и (4), находим связь между скоростью и расстоя­нием, если нам известна величина энергии Е в «начальной» точке А. При эллипти­ческих орбитах Е < 0, потенциальная энергия (по абсолютной величине) больше кинетической.

При параболической орбите скорость в бесконечности будет равна нулю, поэтому она будет соответствовать полной энергии, равной нулю, или Е = 0; отсюда по (3) получаем значение «параболической» скорости в точке A, а именно:

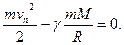(5)

Преобразуя, получаем для v_n написанную выше формулу (2).

При гиперболических орбитах, начинающихся в точке А, энергия Е > О, т. е. кинетическая энергия больше абсолютной величины потенциальной энергии.

Таким образом, формы всевозможных орбит, проходящих через какую-то из­бранную точку А, однозначно связаны с величиной энергии, которой обладает движущееся по ним тело.

Рис.3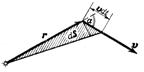

Второй закон Кеплера есть следствие закона сохра­нения момента количества движения. Действительно, на планету, вращающуюся вокруг Солнца, действует сила 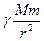тяготения,

всегда направленная к Солнцу, поэтому момент количества движе­ния планеты относительно центра Солнца будет постоянным, т. е.

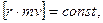
или

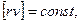(6)

где, как показано на рис.3, r — радиус-вектор, v — вектор ско­рости планеты. Площадь, ометаемая радиусом-вектором за время dt, равна

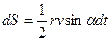
где 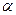— угол между r и v; учитывая выражение (6), можем написать так:

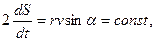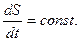или (7)

Из этого закона следует, что при движении по своей орбите планета имеет наибольшую скорость в те моменты, когда она ближе всего к Солнцу (точка А на рис.1).

Трети и закон Кеплера легко доказать, если считать, что орбиты планет являются кругами. В действительности эксцент­риситет орбит эллипсов очень невелик, например, для земной орбиты он составляет ~ 0,017, для орбиты Меркурия ~ 0,205. Заметим, что при точных расчетах, принимая во внимание эксцен­триситет эллиптических орбит, получим тот же результат.

Пусть одна планета имеет массу m₁ круговую орбиту радиуса r₁ и период обращения по орбите T₁, а вторая планета — соответст­венно m₂, r₂, Т₂. Тогда квадрат линейной скорости движения первой планеты по круговой орбите равен:

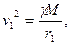
где М — масса Солнца. Скорость движения планеты по орбите равна

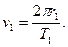
Подставляя это выражение в предыдущую формулу, находим

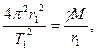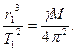или (8)

Точно такое же выражение можно написать и для второй пла­неты:

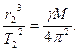(9)

Сравнивая (8) и (9), получаем

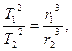
что и представляет содержание третьего закона Кеплера.

Таким образом, механика Ньютона дала полное объяснение законов движения небесных тел. До сих пор продолжаются заме­чательные теоретические исследования астрономами путей движе­ния небесных тел, которые подтверждаются экспериментальными измерениями движения космических кораблей и спутников.

Дата добавления: 2014-01-06