Силы упругости и закон гуна при деформации кручения

Рассмотренный выше сдвиг прямоугольного бруска (парал­лелепипеда) представляет собой однородную деформацию, т. е. относительный сдвиг 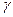для всех параллельных слоев одинаков. Кручение — деформация неоднородного сдвига. Такая деформа­ция возникает в стержне, если закрепить один конец и закручи­вать другой (рис.3). При этом различные сечения стержня будут поворачиваться на различные углы относительно закре­пленного основания стержня. Так, сечение в плоскости а повер­нется на угол , сечение в плоскости b — на угол и т. д. При кручении объем тела не изменяется, так как ни сечение, ни длина стержня не изменяются.

Рис.3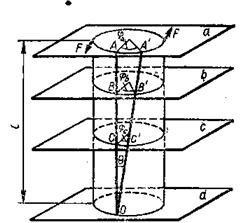

Пусть верхнее сечение повернулось на угол 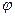(рис.3). Тогда каждая из образующих цилиндрической поверхности (на­пример, образующая ОА) повернется на угол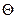, называемый уг­лом сдвига или углом кручения. При малых сдвигах, как видно из рисунка, относительный сдвиг равен:

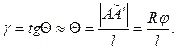
Если мысленно выделить в стержне цилиндрическую поверх­ность меньшего радиуса (r<R), то найдем, что ее элементы испытывают сдвиг (в фиксированнойплоскости а)

меньший, чем элементы на поверхности самого стержня. Таким образом, при кручении элементы стержня испытывают тем боль­шие сдвиги, чем дальше от оси они находятся. Деформация та­кого вида называется неоднородной.

На опыте можно установить, что угол закручивания 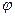верх­него сечения (в плоскости а) пропорционален силе F, приложен­ной по касательной к поверхности стержня в плоскости его сечения а, и радиусу стержня:

Произведение FR = М называют моментом силы. Учитывая это и вводя коэффициент пропорциональности, запишем:

(17)

Значит, угол закручивания верхнего (свободного) сечения стержня прямо пропорционален моменту закручивающей силы, действующему в этом сечении. Величину d называют коэффициентом упругости при деформации кручения. При закручивании возникают внутри стержня уп­ругие силы, которые создают упругий момент М _упр, уравно­вешивающий закручивающий внешний момент М _упр = - М. Из (17) имеем:

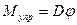(18)

где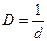— коэффициент уп­ругого (или возвращающего) момента. Для стержня задан­ных размеров он постоянный и может быть определен из опыта. Для этого нужно изме­рить угол закручивания стерж­ня при действии известного момента М и из (17) вычислить 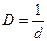. Коэффициент D имеет наименование и размер­ность. Выражения (17) и (18) представляют собой запись закона Гука для деформации сдвига.

Поскольку кручение приводится к деформации сдвига, то ко­эффициент D можно подсчитать и теоретически, выразив его че­рез модуль сдвига и абсолютные размеры стержня. Соответ­ствующий расчет приводит к формуле:

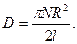(19)

С увеличением радиуса стержня коэффициент возвращающего момента резко растет. Поэтому толстые (и короткие) стержни трудно поддаются закручиванию: уже при малых углах нужны очень большие внешние силы. Наоборот, тонкие и длинные нити под влиянием даже очень малых сил закручиваются на большой угол. Этим обстоятельством пользуются, как уже указывалось, в крутильных весах.

Лекция 16. Диаграмма напряжений. Упругое последействие. Упругий гистерезис. Потенциальная энергия упругой деформации. Плотность энергии.

Дата добавления: 2014-01-06