
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Синус малого угла можно приближенно заменить значением самого угла. В результате получим, что
|
|
|
|
Откуда
sin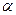 = 0,0035 sin
= 0,0035 sin 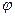 cos
cos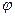 = 0,0018 sin 2
= 0,0018 sin 2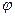 .
.
 (11)
(11)
Таким образом, угол 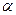 изменяется в пределах от нуля (на экваторе, где
изменяется в пределах от нуля (на экваторе, где 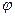 =0, и на полюсах, где
=0, и на полюсах, где 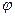 =90°) до 0,0018 рад или 6' (на широте 45°).
=90°) до 0,0018 рад или 6' (на широте 45°).
Направление силы Р совпадает с направлением нити, натянутой грузом; которое называется направлением отвеса или вертикальным направлением. Сила F направлена к центру Земли. Следовательно, вертикаль направлена к центру Земли только на полюсах и на экваторе, отклоняясь на промежуточных широтах на угол
направлена к центру Земли. Следовательно, вертикаль направлена к центру Земли только на полюсах и на экваторе, отклоняясь на промежуточных широтах на угол 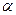 , определяемый выражением (11).
, определяемый выражением (11).
Разность F - Р равна нулю на полюсах и достигает максимума, равного 0,3% силы F
- Р равна нулю на полюсах и достигает максимума, равного 0,3% силы F , на экваторе. Из-за сплюснутости Земли у полюсов сила F
, на экваторе. Из-за сплюснутости Земли у полюсов сила F сама по себе несколько варьирует с широтой, будучи на экваторе примерно на 0,2% меньше, чем у полюсов. В итоге ускорение свободного падения изменяется с широтой в пределах от 9,780 м/с2 на экваторе до 9,832м/с2 на полюсах. Значение g =9,80665 м/с2 принято в качестве нормального (стандартного) значения.
сама по себе несколько варьирует с широтой, будучи на экваторе примерно на 0,2% меньше, чем у полюсов. В итоге ускорение свободного падения изменяется с широтой в пределах от 9,780 м/с2 на экваторе до 9,832м/с2 на полюсах. Значение g =9,80665 м/с2 принято в качестве нормального (стандартного) значения.
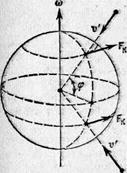
Заметим, что относительно инерциальной, например, гелиоцентрической" системы отсчета свободно падающее тело движется с ускорением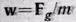 (а не g). Из рис. 5 видно, что из равенства для разных тел ускорения g вытекает и равенство ускорений w. Действительно, треугольники, построенные на векторах Fg и Р для разных тел, подобны (углы а и >
(а не g). Из рис. 5 видно, что из равенства для разных тел ускорения g вытекает и равенство ускорений w. Действительно, треугольники, построенные на векторах Fg и Р для разных тел, подобны (углы а и > 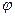 для всех тел в данной точке земной поверхности одинаковы). Следовательно, отношение Fg/P, которое совпадает с отношением
для всех тел в данной точке земной поверхности одинаковы). Следовательно, отношение Fg/P, которое совпадает с отношением 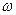 ig, для всех тел одно и то же, откуда вытекает, что при одинаковых g получаются одинаковыми
ig, для всех тел одно и то же, откуда вытекает, что при одинаковых g получаются одинаковыми
и 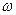 .
.
При движении тела относительно вращающейся системы отсчета, кроме центробежной силы инерции, появляется еще одна сила, называемая силой Кориолис а или кориолисовой силой инерции.
 Рис.6(а,б) Рис.6(а,б)
|
Появление кориолисовой силы можно обнаружить на следующем примере. Возьмем горизонтально расположенный диск, который может вращаться вокруг вертикальной оси. Прочертим на диске радиальную прямую ОА (рис. 6,а ). Запустим в направлении от О к А шарик со скоростью v'. Если диск не вращается, шарик будет катиться вдоль прочерченной нами прямой. Если же диск привести во вращение в направлении, указанном стрелкой, то шарик будет катиться по изображенной пунктиром кривой ОВ, причем его скорость относительно диска v' будет изменять свое направление. Следовательно, по отношению к вращающейся системе отсчета шарик ведет себя так, как если бы на него действовала сила FK, перпендикулярная к скорости v'
Чтобы заставить шарик катиться по вращающемуся диску вдоль радиальной прямой, нужно сделать направляющую, например, в виде ребра О А (рис. 6,б). При качении шарика направляющее ребро действует на него с некоторой силой Fr. Относительно вращающейся системы (диска) шарик движется с постоянной по направлению скоростью. Это можно формально объяснить тем, что сила Fr уравновешивается приложенной к шарику силой инерции FK, перпендикулярной к скорости v'. Сила FK и есть кориолисова сила инерции.
Найдем сначала выражение силы Кориолиса для частного случая, когда частица т движется относительно вращающейся системы отсчета равномерно по окружности,
 Рис.7 Рис.7
|
лежащей в плоскости, перпендикулярной к оси вращения, с центром, находящимся на этой оси (рис. 7). Скорость частицы относительно вращающейся системы обозначим v'. Скорость частицы относительно неподвижной (инерциальной) системы отсчета v равна по величине  +
+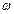 R в случае (а) и |
R в случае (а) и | -
-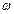 R
R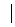 в случае (б), где — угловая скорость вращающейся системы,R — радиус окружности.
в случае (б), где — угловая скорость вращающейся системы,R — радиус окружности.
Для того чтобы частица двигалась относительно неподвижной системы по окружности со скоростью 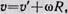 на нее должна действовать направленная к центру окружности сила F, например, сила натяжения нити, которой частица привязана к центру окружности (см. рис. 7 ). Величина этой силы равна
на нее должна действовать направленная к центру окружности сила F, например, сила натяжения нити, которой частица привязана к центру окружности (см. рис. 7 ). Величина этой силы равна
F=m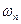 =
=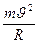 =
= =
= +2m
+2m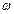
 + m
+ m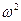 R (12)
R (12)
Относительно вращающейся системы частица в этом случае движется с ускорением 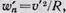 т. е. так, как если бы на нее действовала сила
т. е. так, как если бы на нее действовала сила
 (13)
(13)
Таким образом, во вращающейся системе частица ведет себя так, как если бы на нее, кроме направленной к центру окружности силы F, действовали еще две направленные от центра силы: 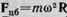 и сила Fk, модуль которой равен 2m
и сила Fk, модуль которой равен 2m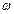
 (рис. 7) Cилу FK можно представить в виде
(рис. 7) Cилу FK можно представить в виде
 (14)
(14)
Сила (14) и есть кориолисова сила инерции. При v'=0 эта сила отсутствует. Сила Fu6 не зависит от v' — она, как мы уже отмечали, действует как на покоящиеся, так и на движущиеся тела. В случае, изображенном на рис. 7
F=m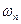 =
=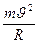 =
= =
= -2m
-2m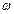
 + m
+ m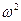 R
R
Соответственно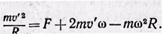
Следовательно, во вращающейся системе частица ведет себя так, как если бы на нее действовали две направленные к центру окружности силы: F и Fk, а также направленная от центра сила Fu6=m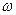 2R. Сила Fk и в этом случае может быть представлена в виде (14).
2R. Сила Fk и в этом случае может быть представлена в виде (14).
Теперь перейдем к нахождению выражения силы Кориолиса для случая, когда частица движется относительно вращающейся системы отсчета произвольным образом. Свяжем с вращающейся системой координатные оси х', y', z', причем ось , z' совместим с осью вращения (рис. 8). Тогда радиус-вектор частицы можно представить в виде  (15)
(15)

|
Рис.8
_
Положение частицы относительно неподвижной системы следует определять с помощью радиуса-вектора г. Однако символы г' и г обозначают один и тот же вектор, проведенный из начала координат к частице. Символом г' обозначил этот вектор наблюдатель, «живущий» во вращающейся системе отсчета; по его наблюдениям орты  , е'у, е'г неподвижны, поэтому при дифференцировании выражения (15) он обращается с этими ортами как с константами. Символом г пользуется неподвижный наблюдатель; для него орты
, е'у, е'г неподвижны, поэтому при дифференцировании выражения (15) он обращается с этими ортами как с константами. Символом г пользуется неподвижный наблюдатель; для него орты , е'у, вращаются со скоростью
, е'у, вращаются со скоростью 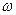 (орт e'z неподвижен). Поэтому при дифференцировании равного г выражения (15) неподвижный наблюдатель должен обращаться с
(орт e'z неподвижен). Поэтому при дифференцировании равного г выражения (15) неподвижный наблюдатель должен обращаться с  и е'у как с функциями t, производные которых равны:
и е'у как с функциями t, производные которых равны:
 (16)
(16)
| Для вторых производных ортов по времени получаются выражения:
 (17)
(17)
Найдем скорость частицы относительно вращающейся системы отсчета. Для этого продифференцируем радиус-вектор (15) по времени, считая орты константами
Повторное дифференцирование этого выражения даст ускорение частицы относительно вращающейся системы отсчета:
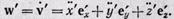 (18)
(18)
Теперь найдем скорость частицы относительно неподвижной системы отсчета. Для этого продифференцируем радиус-вектор (15) «с позиций» неподвижного наблюдателя. Воспользовавшись обозначением г вместо г' (напомним, что г=г'), получим:
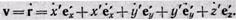 (19)
(19)
Продифференцировав это выражение еще раз по t, найдем ускорение частицы относительно неподвижной системы. Приняв во внимание формулы (15), (16) и (18), полученное соотношение можно преобразовать к виду:
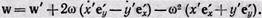 (20)
(20)
Соотношение (20) можно записать следующим образом:
 (21)
(21)
Из (21) вытекает, что ускорение частицы относительно неподвижной системы отсчета можно представить в виде суммы трех ускорений: ускорения относительно вращающейся системы w',
ускорения, равного —  R1), и ускорения
R1), и ускорения
wK=2[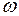 , v'],которое называется кориолисовым ускорением.
, v'],которое называется кориолисовым ускорением.
Для того чтобы частица двигалась с ускорением (21), на нее должны действовать какие-то тела с результирующей силой F=mw. Согласно (21)
mwr = mw - 2m[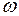 , v'] + m
, v'] + m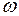 2R = F + 2m[v',
2R = F + 2m[v', 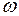 ] + m
] + m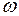 2R (22)
2R (22)
(перестановка сомножителей изменяет знак векторного произведения}. Полученный результат означает, что при составлении уравнения второго закона Ньютона во вращающейся системе отсчета,
|

|
кроме сил взаимодействия, нужно учитывать центробежную силу инерции, а также кориолисову силу. Отметим, что сила Кориолиса всегда лежит в плоскости, перпендикулярной к оси вращения.
Из сопоставления формул (19), (17), (15), и что с помощью выкладок, аналогичных тем, которые привели нас к соотношению (21), можно убедиться в том, что
V=v'+[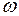 , r']. (23)
, r']. (23)
 Примеры движений, в которых проявляется кориолисова сила инерции. При истолковании явлений, связанных с движением тел относительно земной поверхности, в ряде случаев необходимо учитывать влияние кориолисовых сил. Например, при свободном падении тел на них действует кориолисова сила, обуславливающая отклонение к востоку от линии отвеса (рис.9). Эта сила максимальна на экваторе и обращается в нуль на полюсах.
Примеры движений, в которых проявляется кориолисова сила инерции. При истолковании явлений, связанных с движением тел относительно земной поверхности, в ряде случаев необходимо учитывать влияние кориолисовых сил. Например, при свободном падении тел на них действует кориолисова сила, обуславливающая отклонение к востоку от линии отвеса (рис.9). Эта сила максимальна на экваторе и обращается в нуль на полюсах.
|
| Рис. 11. |
Летящий снаряд также испытывает отклонения, обусловленные кориолисовыми силами инерции (рис.10). При выстреле из орудия, направленного на север, снаряд будет отклоняться к востоку в северном полушарии и к западу — в южном. При стрельбе вдоль меридиана на юг направления отклонения будут противоположными. При стрельбе вдоль экватора силы Кориолиса будут прижимать снаряд к Земле, если выстрел произведен в направлении на запад, и поднимать его кверху, если выстрел произведен в восточном направлении. Предоставляем читателю самому убедиться в том, что сила Кориолиса, действующая на тело, движущееся вдоль меридиана в любом направлении (на север или на юг), направлена по отношению к направлению движения вправо в северном полушарии и влево в южном полушарии. Это приводит к тому, что у рек подмывается всегда правый берег в северном полушарии и левый берег в южном полушарии. Эти же причины объясняют неодинаковый износ рельсов при двухколейном движении.
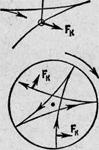
Силы Кориолиса проявляются и при качаниях маятника. На рис. 11 показана траектория груза маятника (для простоты предположено, что маятник находится на полюсе). На северном полюсе сила Кориолиса будет все время направлена вправо по ходу маятника, на южном полюсе — влево. В итоге траектория имеет вид розетки.
Как следует из рисунка, плоскость качаний маятника поворачивается относительно Земли в направлении часовой стрелки, причем за сутки она совершает один оборот. Относительно гелиоцентрической системы отсчета дело обстоит так, что плоскость качаний остается неизменной, а Земля поворачивается относительно нее, делая за сутки один оборот. Можно показать, что на широте ф плоскость качаний маятника поворачивается за сутки на угол 2я sin ф.
Таким образом, наблюдения за вращением плоскости качаний маятника (маятники, предназначенные для этой цели, называются маятниками Фуко) дают непосредственное доказательство вращения Земли вокруг своей оси.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 3749; Нарушение авторских прав?; Мы поможем в написании вашей работы!